Tunable Floating-Point Multiplier

Alberto Nannarellii

DTU Compute, Technical University of Denmark
Kongens Lyngby, Denmark
Email: alna@dtu.dk

Abstract

In this report, we address the design of a multiplier in Tunable Floating-Point (TFP) precision for use in on-chip accelerators. The precision can be chosen for a single operation by selecting a specific number of bits for significand and exponent in the floating-point representation. By tuning the precision of a given algorithm to the minimum precision achieving an acceptable target error, we can make the computation more power efficient.

1  Introduction

In this work, we address the design of an on-chip accelerator with Tunable Floating-Point (TFP) precision. That is, the precision of operands and results can be chosen for a single operation by selecting a specific number of bits for significand and exponent in the floating-point representation.
By tuning the precision of a given algorithm to the minimum precision achieving an acceptable target error, we can make the computation more power efficient. In this work, we focus on floating-point multiplication, which is the more power demanding arithmetic operation.
We present a Tunable Floating-Point multiplier (TFP-mult) which can be used as part of on-chip accelerators. The TFP-mult can handle significand precision from 24 to 4 bits, and exponent from 8 to 5 bits. The maximum precision (m=24, e=8) is that of binary32 (single-precision), and the tunable range includes binary16, or half-precision, (m=11, e=5).
The main features of the TFP multiplier are:
  1. Providing correct rounding when reducing the precision of the significands.
  2. The precision of the significand m and the exponent range e can be changed on a cycle basis.
The goal is to obtain a power efficient multiplier by trading off accuracy (precision) and energy.

2  Tunable Floating-Point

The floating-point representation of a real number x is
x = (−1)Sx ·Mx ·bEx         x ∈ ℜ
where Sx is the sign, Mx is the significand or mantissa (represented by m bits), b is the base (b=2 in the following), and Ex is the exponent (represented by e bits). The representation in the IEEE 745-2008 standard [1] has significand normalized 1.0 ≤ Mx < 2.0 and biased exponent: bias = 2e−1−1.
The formats for binary floating-point in IEEE 745-2008 are specified in Table 1 [1].
Binary formats
Format binary16 binary32 binary64 binary128
Storage (bits) 16 32 64 128
Precision m (bits) 11 24 53 113
Total exponent length e (bits) 5 8 11 15
Emax 15 127 1023 16383
bias 15 127 1023 16383
Trailing significand f (bits) 10 23 52 112
Table 1: Binary formats in IEEE 754-2008 [1].
The dynamic range1 for binary floating-point (BFP) is
DRBFP = (2m−1)·22e−1  .
For example, for binary32 (m=24, e=8)
DRb32 = (224−1)228−1 ≈ 9.7 ×1083
which is much larger than the dinamic range of the 32-bit fixed-point representation:
DRFXP = 232−1 ≈ 4.3 ×109 [2].
For the Tunable Floating-Point (TFP) representation, we only consider dynamic ranges from and below the binary32 representation. We support significand's bit-width from 24 to 4 and exponent's bit-width from 8 to 5. Table 2 shows the dynamic ranges for some TFP cases.
storage
meDRbits∗ comment
24 8 9.7 ×1083 32 binary32
11 8 1.2 ×1080 19
4 8 8.7 ×1077 12
24 5 3.6 ×1016 29
11 5 4.4 ×1012 16 binary16
4 5 3.2 ×1010 9
1665,536 16 16-bit FXP
∗ It includes the sign bit.
Table 2: Dynamic range for some TFP formats.
By comparing TFP with FXP ranges, the TFP ones are much larger than the FXP for similar bits of storage. This is advantageous especially for multiplication for which the dynamic range increases quadratically. As for the significand's precision, the optimal bit-width depends on the application.
We assume that the TFP representation is normalized to have the conversions compatible with the IEEE 754-2008 standard. Therefore, the implicit (integer) bit is not stored. Subnormals support is quite expensive for multiplication, and, therefore, we opted to flush-to-zero TFP numbers when the exponent is less than −(Emax−1).
As for the rounding, TFP supports three types:

3  TFP Multiplier

3.1  Baseline FP Multiplier

The starting point is a generic floating-point multiplier. The architecture of the significand computation is sketched in Figure 1. We assume the FP-operands to be normalized and subnormals are flushed to zero. The implicit (integer) bit is already included in Figure 1.
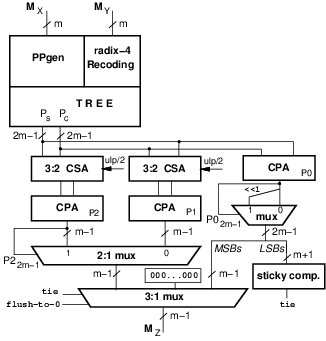
Figure 1: Significand computation in FP multiplier (for binary32 m=24).
The radix-4 partial products (PPs) are added in a carry-save adder tree to produce PS and PC. Because of the normalization, the product is in the range 1.0 ≤ P < 4.0 and may require normalization (1 position right shift). As normally done for a faster operation, the rounding is performed speculatively by adding [ulp/2] in the two adjacent position m and m−1 as illustrated in Figure 2. This speculative rounding is implemented by the pairs CSA-CPA3 producing P2 and P1. Depending on the position of the leading one (position 2m−1 or 2m−2 in Figure 2) the normalized and rounded product is selected.
pos. 2m-12m-22m-3… m+2 m+1 m m-1 m-2 … 10
P2:1b   .   b… bLRbb… b b
ulp/2:1
P1:01   .   b … bb LRb… b b
ulp/2:1

Figure 2: Speculative rounding for m-bit significands.
To support roundTiesToEven, we need to compute the sticky bit
T = ORi=0m−1 bi
For each of the cases in Figure 2, if L=0, T=0 and R=1 the bit to be added for rounding is 0. To include this case of rounding, we need to include a third adder which adds PS+PC (CPA P0 in Figure 1).
Moreover, if the biased exponent is 0 (subnormal or zero) or 2e−1 (infinity), we need to flush the signicand to zero.
The final selection of the significand is done taking into account the leading one in P2 (or P0), the roundTiesToEven condition tie and the exponent flag flush-to-0.
The architecture of Figure 1 can be optimized by sharing parts of the datapaths (addition of the m−1 least-significant bits, LSBs) and by using compound adders [2], or by many other methods in the literature [3].
The hardware to compute the exponent is sketched in Figure 3. It consists in the exponents addition
E1 = Ex + Ey − Bias
followed by the speculative increment E2=E1+1 in case the significand needs normalization (P2(47)=OVF=1). In parallel to the exponent addition, the implicit bit is computed: Mi(m)=0 if Ei=0.
To ensure the exponent is in the allowed range, E1, or E2, is checked against 0 and Emax. The final exponent Ez is set depending on the signals INFTY (infinity) or ZERO (zero and subnormals), and, for the significand selection:
flush−to−0 = ZERO   OR   INFTY
The sign is computed by a simple XOR-gate:
Sz = Sx ⊕Sy .
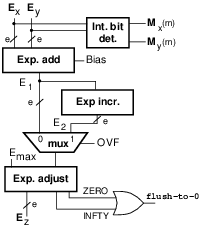
Figure 3: Exponent computation in FP multiplier (for binary32 e=8).

3.2  Hardware Support for Tunable FP

In this section, we explain how to augment the unit of Figure 1 and Figure 3 to support TFP.
For the significand computation, the challenge is to inject the rounding bit in position r so that the m resulting bits of the significand are correctly rounded. For example, as illustrated in Figure 4, for the datapath of Figure 1 (the MSB of P2 is 47 for binary32), if the required precision is m=11, the rounding bit is in position r=36 if the leading one in P2 is in position 47.
pos. 474645444342414039383736353433… 25242322…
P2:1bbbbbbbbbLRbbb… 0 0 00…
RW:000000000001000… 0 0
SB:---------------… -LRb…
Figure 4: Example of "rounding word" (RW), and selection (SB) for sticky-bit computation for m=11.
Therefore, to correctly round the TFP significand with arbitrary m, we need to augment the hardware as follows.
1) Add a decoder to generate the "rounding word" (RW) depending on m. By setting m > 24, the decoder selects RW=0 to implement RTZ (truncation).
2) Add a variable shift-right unit to select the proper bits for the sticky bit computation. Since the sticky comp. unit of Figure 1 reads the m+1=25 LSBs for binary32, for a different m, we have to shift to the right the significand so that bit L moves to position 24 (MSB) of sticky comp.. The shifting amount is SHAMT=24−m. For the example of Figure 4, m=11, L is in position 37, and by shifting right by 24-11=13 positions we obtain the correct selection.
3) Add a mask in the m-MSB of the 3:1 mux to zero the m LSBs of the product.
This mask can be generated by the decoder. For example for m=11: 
    RW:    0000 0000 0001 0000 0000 0000

    MASK:  1111 1111 1110 0000 0000 0000
The modified datapath supporting TFP m=[4,24] for significand computation is depicted in Figure 5. The added or modified parts are in color in the figure.
Figure 5: Significand computation to support TFP multiplication.
The exponent computation in TFP is less complicated than the significand one. The range of supported exponents is e=[5,8] to comprise the binary16 and binary32 formats.
The bias (B), equal to Emax, can be obtained by simple logic as in Table 3 from the 2-LSBs of e:
B6 =
e1 + e0
 
 ,   B5 =
e1 ⊕e0
 
 ,   B4 = e1 +
eo
 
  .
e (bits) Bias (bits)
e e3 e2 e1 e0 Bias B7 B6 B5 B4 B3B2B1B0
5 0101 15 0000 1111
6 0110 31 0001 1111
7 0111 63 0011 1111
8 1000 1270111 1111
Table 3: Table to generate bias.
The remaining parts of Figure 3 are not changed.
Since the TFP-unit can accommodate up to binary32, when m < 24 or e < 8, the (24-m)-LSBs of the significand are zero and the (8-e)-MSBs of the exponent are meaningless.
The significand and exponent bit-widths m and e can be selected for the single operation by setting a 7-bit value in a control register (not depicted in Figure 5).

4  Hardware Implementation

For the implementation of the multiplier we opted for a 45 nm CMOS library of standard cells by using commercial synthesis and place-and-route tools (Synopsys). The FO4 delay4 for this low power library is 64 ps and the area of the NAND-2 gate is 1.06 μm2.
We set as a target clock period a delay of about 15 FO4 which is comparable to the clock cycle of industrial designs: 17 FO4 in [4]. Therefore, since 15 FO4 ≅ 1.0 ns, the target throughput is 1 GFLOPS for a single TFP multiplier.
To reach the target clock period, the architecture of Figure 5 must be pipelined in two stages, with pipeline registers placed after the adder tree (PS and PC) for the significand datapath.
We evaluated the implementation of two variants: one with roundTiesToEven (RTNE) rounding mode, the other with round to the nearest (RTN) mode.
The RTN unit, with respect to Figure 5, does not require the blocks CPA (P0), the shifter, and the sticky bit computation. Moreover, the selection logic is simplified. The RTN unit (significand plus exponent datapaths) is shown in Figure 6. The blue horizontal cut indicates the position of the pipeline registers (same placement for both units).
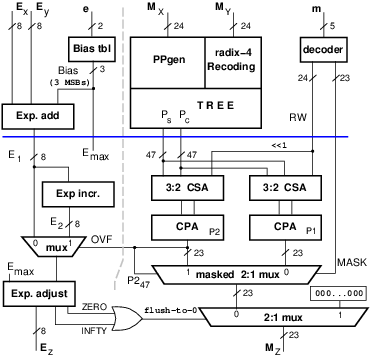
Figure 6: TFP multiplier (RTN variant).
A post-synthesis comparison of two units is reported in Table 4.
RTN RTNE difference
max. delay [ps] 944 945
 
AREA [NAND2 equiv.]
combinational 11,540 13,760 +20%
registers 1,320 1,320 -
Total 12,860 15,080 +17%
 
Total power [mW] 18.98 21.57 +14%
Table 4: Post synthesis comparison between RTN and RTNE TFP-mult.
The delay of the critical is identical and both units meet the timing constraint of TC=1.0 ns. The area in the functional blocks of RTNE is about 20% larger than in the RTN unit. This overhead is reduced to about +17% when the input and pipeline registers are accounted for. The power dissipation is measured at frequency 1 GHz for binary32 operands (worst case). The power overhead for the RTNE unit is about 14%.
The TFP multiplier is intended to be used in accelerators as an element of a multi-lane vector unit. Although the overheads are not very large, for a given area or power footprint we can fit more RTN units. For example, if the power budget is 150 mW we can fit 8 RTN-mults vs. 7 RTNE-mults.
Moreover, the error analysis done for the case of matrix multiplication, reported in Figure 7, suggests that the difference between the RTN and RTNE rounding modes is not critical. For these reasons, we selected the RTN unit of Figure 6 for the evaluation of the power efficiency by TFP.
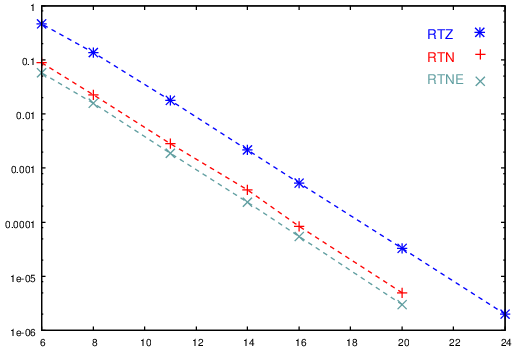
Figure 7: Average error for 50×50 matrix multiplication under TFP rounding modes.

4.1  TFP Multiplier Experiments

To have a more accurate evaluation, we built the layout for a single TFP RTN-mult of Figure 6. The post-layout timing and area resulted to be better than the estimates of Table 4: the delay of the critical path changed to 943 ps (almost identical), but the total area is reduced to 10,930 NAND2 equivalent gates, about 15% less than the post-synthesis estimate. This reduction has a positive effect on the power dissipation as explained next.
For the power dissipation, we created traces for the execution of two algorithms: matrix multiplication and Gaussian elimination. We sampled several m and e values for the two algorithms, and we run post-layout simulations (Synopsys VCS) for several test cases.
By comparing power figures for the same m, but different exponent bit-width e, we noticed a small difference. The reason is that most of the power in a FP multiplier is dissipated in the significand computation. For example by comparing e=8 and e=5 for m=11, the difference in power dissipation in the exponent path is less than 30%. However, the exponent path impacts less than 3% the total power of the TFP-mult with m=11. Therefore, from a power dissipation point of view, going from e=8 to e=5 results in a overall power reduction of less than 1%.
Since the power savings in reducing the exponent bit-width are not significant, and to simplify the presentation of the experimental results, we opted for test patterns with fixed exponent e=8.
For the two algorithms, we run post-layout power estimation for the following significand bit-widths:
The results for the total average power dissipation are reported in Table 5 and plotted (together with the trends) in Figure 8.
Matrix multiplication Gauss elimination
m Pave [mW] ratio Pave [mW] ratio
24 		10.83 1.00 12.67 1.00
20 10.77 0.99 11.58 0.91
16 10.70 0.99 9.79 0.77
14 10.11 0.93 9.23 0.73
11 8.50 0.78 7.87 0.62
9 6.47 0.51
8 6.10 0.56
6 5.11 0.47
Pave measured at 1 GHz.
Table 5: Average power dissipation for TFP-mult (RTN) as m scales (e=8).
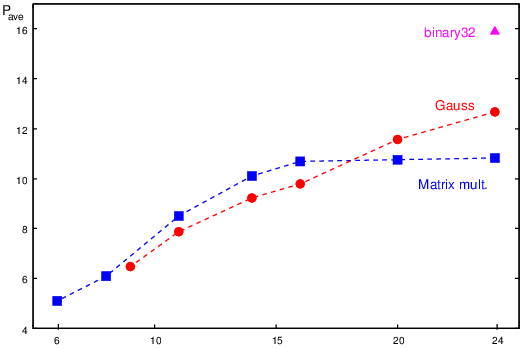
Figure 8: Trends of average power dissipation for TFP-mult (RTN) as m scales (e=8).
The average power dissipation, estimated post-layout, for binary32 operands (not reported in Table 5) is 15.92 mW at 1 GHz. The smaller value with respect to the post-synthesis estimation, 18.98 mW in Table 4, is due to the denser actual layout than the estimated one. Consequently, the switched capacitance is reduced and so it is the power dissipation.
The trends in Figure 8 show a flat power dissipation from m=24 to m=16 for the matrix multiplication algorithm. The reason is that the operands dynamic range (matrices' elements) is limited to 16 bits in our experiments. As a consequence, in the TFP-mult the 8 LSBs of the operands are zero and the switching activity in the PPs generation and adder tree is significantly reduced with respect to the case of binary32 where all bits of the datapath are stimulated.
In summary, the results of Table 5 show that by using TFP multipliers we can achieve a good power efficiency and maintain correct rounding to achieve the target error.

5  Conclusions and Future Work

In this report, we presented a Tunable Floating-Point representation to reduce precision and dynamic range of floating-point numbers when the rounding error produces still acceptable results. The main purpose of TFP is to reduce the energy footprint of accelerators by introducing flexibility in the choice of significand and exponent bit-widths.
The main contribution is the design of a TFP multiplier providing correct rounding for the selected precision, and reduced power dissipation. The TFP-mult can be deployed in an array to form a multi-lane multiplier.
In presenting the results of two simple algorithms implemented, we opted for a simple round-to-the-nearest (RTN) unit. However, in future work, we plan to implement a TFP-mult supporting IEEE 754' roundTiesToEven (RTNE) and make programmable the rounding mode by disabling the blocks not used in a specific mode. In this way, we can increase the flexibility of the accelerator and keep a good power efficiency.
We also plan to extend TFP to the other operations: addition, division and square root.

References

[1]
IEEE Standard for Floating-Point Arithmetic, IEEE Computer Society Std. 754, 2008.
[2]
M. Ercegovac and T. Lang, Digital Arithmetic.    Morgan Kaufmann Publishers, 2004.
[3]
E. M. Schwarz, R. M. A. III, and L. J. Sigal, "A radix-8 CMOS S/390 multiplier," in Proc. 13th IEEE Symposium on Computer Arithmetic (ARITH), July 1997, pp. 2-9.
[4]
N. Burgess and C. N. Hinds, "Design of the ARM VFP11 Divide and Square Root Synthesisable Macrocell," Proc. of 18th IEEE Symposium on Computer Arithmetic, pp. 87-96, July 2007.

Footnotes:

1The dynamic range is the ratio between the largest and the smallest (non-zero and positive) number [2].
2ulp is the unit in the last position.
3 CSA: carry-save adder. CPA: carry-propagate adder.
4A 1 FO4 delay is the delay of an inverter of minimum size with a load of four minimum sized inverters.

File translated from TEX by TTH, version 4.06.
On 15 Mar 2018, 15:14.