Copyright 2001 IEEE. Published in the Proceedings of 13th International Conference on Application-specific Systems, Architectures and Processors (ASAP 2002), p. 185-196, San Jose, California (USA), July 17-19, 2002.

Fast Radix-4 Retimed Division with Selection by Comparisons ¹

Elisardo Antelo¹, Tomás Lang², Paolo Montuschi³ and Alberto Nannarelli⁴
 

Abstract

1  Introduction

Digit-recurrence division is an algorithm in which the quotient is obtained one digit per iteration. This algorithm has been extensively studied (for additional references see for instance [1]) and provides good tradeoff among latency, area, and power, allows simple exact rounding, and does not introduce overhead on the floating-point multiplier. It has been implemented in many high-performance floating-point units for general-purpose and application-specific processors, such as processors for 3D graphic applications ; some recent examples are described in [2,,,].

The determination of the quotient digit is performed by the quotient-digit selection function. The prevalent method used today for this quotient-digit selection is to use selection constants and implement it by a combinational network having as inputs a truncated redundant residual and a truncated divisor. Because of the delay/complexity of this network, this approach is practical for relatively small radices, mainly radix 4 and possibly up to radix 8. An alternative implementation is based on comparisons of the residual estimate with truncated multiples of the divisor; however, this implementation is rarely used in practice because it requires assimilation of the truncated redundant residual and comparison, so no advantage is obtained with respect to the implementation with selection constants.

Recently [6], a scheme was described that uses the selection function with selection constants but implements it with comparisons ². Specifically, since the divisor is fixed during all the iterations, the selection constants corresponding to the value of the truncated divisor are preloaded into registers and the quotient-digit selection is performed by comparing the truncated residual with the selection constants. To reduce the delay, the comparisons are implemented by a carry-free subtraction of the selection constants from the redundant residual and then performing a sign detection. From the synthesis we performed we estimate that for radix 4 this results in a delay reduction of about 5% with respect to the direct implementation. In this paper, we propose to utilize this decomposition of the comparison into redundant subtraction and sign detection and to retime the recurrence so that the subtraction is not part of the critical path. We have estimated the resulting delay and obtained an additional 30% reduction. Moreover, we estimate that the area of the three implementations is almost the same.

In the next sections we present the modified algorithm, discuss the timing alternatives for minimal delay, and do and estimation of the delay.

2  Proposed selection function implementation

Digit-by-digit radix-r division algorithms compute the final result by performing a suitable number of iterations, each one consisting of the following phases:

1. Quotient-Digit Selection: based on the value of the current residual and of the divisor one digit of the quotient is produced. If a redundant digit set is used for the quotient, estimates of the shifted residual (denoted by [^y]) and of the divisor ([^d]) can be used, resulting in
   

   qj+1 = sel( ^ y   , ^ d   )

   The prevalent method to perform the quotient-digit selection uses selection constants m_i,k such that
   

   qj+1 = k if  ^ d   = 2-1+i ×2-d and mi,k £ ^ y   < mi,k+1 for 0 £ i £ 2d-1-1

   where -a £ k £ a, [^d] is the truncated divisor with d fractional bits, and [^y] is the truncated shifted residual (rw[j]) with t fractional bits.

2. Residual Updating and Quotient Formation: using the digit selected at step 1, the next residual and quotient are produced, as follows:
   

   w[j+1] = rw[j]-qj+1d

   
   

   Q[j+1] = Q[j] + qj+1r-(j+1)

   To reduce the delay of an iteration a redundant adder (carry-save or signed digit) is used for this residual updating. Moreover, the conversion of the quotient to conventional representation can be done on-the-fly [1].

The implementation of the recurrence for radix-4 is shown in Figure 1. Note that we present a retimed version in which the quotient-digit selection is placed at the end of the iteration since this constrains the critical path to the most-significant slice, which can be designed for smaller delay. This retiming was used in [7], where it is called model division with prediction, and in [8], to reduce the energy dissipation. The retimed version allows us to speed up the scheme proposed in [6].

Although it is possible to define correct digit selection rules for any radix, the approach is practical only for relatively low radices, such as 2, 4, and 8, because for higher radices the resulting implementation has a large area and delay. For this reason, for higher radices alternative techniques have been studied, such as multistage algorithms and/or prescaling.

The prevalent implementation of the selection function above consists of a combinational network (multilevel network, PLA or ROM) having as inputs the estimate of the residual and of the divisor and producing the quotient digit. For instance, for radix 4 with a quotient digit-set {-2,-1,0,1,2}, 7 bits of [^y] and 3 bits of [^d] are sufficient (see Figure 1). Typically, the selection network is implemented as shown in Figure 2a) and its delay corresponds to about 50% of the iteration delay.

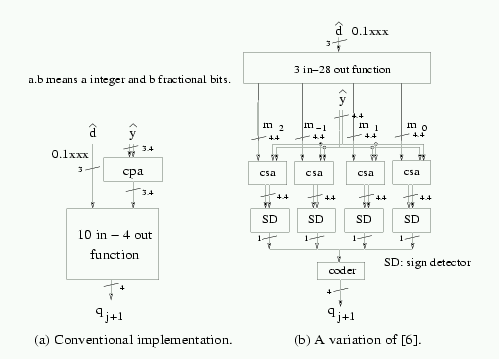Recently [6] a scheme was described to implement the quotient-digit selection by preloading the selection constants corresponding to [^d] (which does not change for the whole operation) and performing the selection using comparisons (see Figure 2b³). Specifically, the algorithm consists in

1. Preloading the selection constants. Let us call the preloaded constants⁴ m_k.

2. Perform the comparison in two steps:

   1. produce z_k = [^y] - m_k. This subtraction is done with redundant adders.

   2. perform the comparison by a sign detection of z_k.

Based on our synthesis results (see Section 4) this scheme does not produce a significant speed up as compared to the standard algorithm.

Proposed implementation

Specifically, since

w[j] = rw[j-1] - qjd

we have⁵

^ y   - mk = ë rw[j] ût- mk = ë r2w[j-1]-rqjd ût-mk

Since we use carry-save representation, the previous computation is performed in two separate truncation steps with one additional fractional bit

^ y   -mk = ë ër2w[j-1] ût+1 + ë-rqjd ût+1 ût - mk

that is, using the truncated r²w[j-1] and the truncated -rq_jd. Moreover, since m_k has t fractional bits we may perform the computation as follows

^ y   -mk = ë [ër2w[j-1] ût+1 -mk ] + ë-rqjd ût+1 ût

(1)

In this way the computation of ër²w[j-1] û_t+1 -m_k is outside of the critical path.

2.1  Number of bits

The number of fractional bits of the various signals is as described by expression (1). We now consider the number of integer bits, which corresponds to the maximum value of |[^y] -m_k|. Since,

m- = mmax(i),-(a-1) £ mi,k £ mmaxi,a = m+

from [1], these maximum values are

max (| ^ y   -mk|) = max (ërrût+|m-|, | ë-rr-2-t ût-m+|)

Radix-4 minimally redundant digit set

This means that 4 integer bits are necessary for performing a correct sign comparison, i.e. one more than the number of integer bits required to represent [^y] in the "classical" algorithm.

Reduction in the number of bits of [^y]-m_k

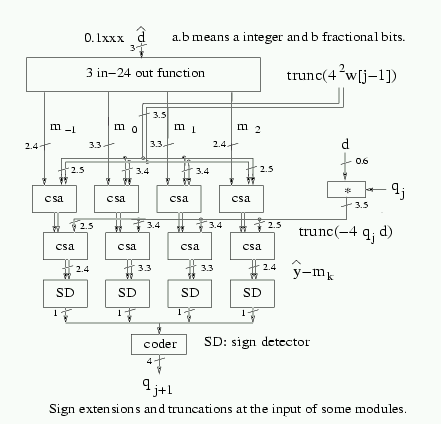
According to the discussion above, the number of bits of [^y]-m_k is of four integer bits and four fractional bits, for a total of eight bits. We have performed a more detailed analysis to reduce this number to six. This reduction is based on the following considerations:

1. As shown in Table 1, for some ranges of values of [^y] some of the outputs of the SD modules are not used in the determination of the quotient digit. In the Table we denote by [L, H] the interval of values of [^y] and by x the dont cares. Note that the values of H, L, and m_k depend on [^d].

   Table 1: Reduction of number of bits.

   [^y]	SD2	SD1	SD0	SD-1
   [m2,H]	+	+	+	x	q = 2   if (SD2,SD1)    = (+,+)
   [m1,m2)	-	+	+	x	q = 1   if (SD2,SD1)    = (-,+)
   [m0,m1)	x	-	+	x	q = 0   if (SD1,SD0)    = (-,+)
   [m-1,m0)	x	-	-	+	q = -1 if (SD0,SD-1) = (-,+)
   [L,m-1)	x	-	-	-	q = -2 if (SD0,SD-1) = (-,-)
   [^y]-mk	[m1-m2,	[L-m1,	[L-m0,	[L-m-1,
   	H-m2]	H-m1]	H-m0]	m0-m-1]
   max(|[^y]-mk|)	1.25	3.25	3.125	1.312
   Integer bits	2	3	3	2

2. Considering the most positive and most negative values (not dont cares) we determine the maximum magnitudes of [^y]-m_k. The corresponding values are given in the table (see details in [9]) together with the required number of integer bits.

With respect ot the number of fractional bits:

• For [^y]-m₂, four bits are required because m₂ can take the value 15/16.
• For [^y]-m₁, it might be possible to use three bits, because all m₁ are multiples of 1/8. However, this requires the use of t = 3 so it is necessary to determine whether constants which are multiples of 1/8 are still possible for t = 3. As described in [9], only for [^d] = 8/16 this is not possible; however this can be solved by adding 1/16 to the corresponding rw[j] and this addition can be achieved by augmenting the constant m₁ by 1/16 for that value of [^d].
• For [^y]-m₀ also 3 fractional bits can be used since all m₀ are multiples of 1/8. Again this requires the addition of 1/16 to the constant m₀ for [^d] = 8/16.
• For [^y]-m_-1 four fractional bits are needed because m_-1 can take the value -15/16.

In summary, Table 2 gives the required number of integer and fractional bits of [^y]-m_k.

2.2  Implementation of the quotient-digit selection

3  Timing and Complete Algorithm

3.1  Timing

The iterations described in the previous section are executed either by a combinational network (if all iterations are unfolded) or by a sequential system, in which a part is executed each cycle. We consider this second approach, for the case where one iteration is performed per cycle.

The corresponding sequential system requires the introduction of registers that store the state between cycles. The placement of these registers has an effect on the minimum cycle time and on the area and energy of the implementation. We describe now a method to analyze the cycle time for the particular algorithm of the previous section.

The process begins with a dependency graph of the algorithm. In Figure 4(a) we show this graph for two iterations⁶, so that we can place the registers that define a complete cycle. We place registers in both iterations, but the corresponding registers of both iterations are implemented as a single register in the sequential system. To simplify the description of the analysis, we label the nodes A to F, resulting in the graph of Figure 4(b).

In the graph we identify four paths labeled P1 to P4. To produce a sequential system we have to introduce registers to cut these paths, once per iteration. Consequently, a maximum of four registers are needed. However, we see that the paths are not disjoint, so that one register can be used to cut more than one path. In this particular algorithm, paths P1 and P3 intersect at node E and paths P2 and P4 at node F. Therefore, there are the following four possibilities in the placement of registers:

1. Two registers, one in node E and one on node F.
2. Three registers, one on node E, one on node C, and one on node D.
3. Three registers, one on node F, one on node A, and one on node B.
4. Four registers, one on each of the nodes A,B,C and D.

Now we consider the cycle time⁷. The minimum value is obtained by the maximum delay of all the paths between registers of the two iterations. Consequently, the minimum cycle time is obtained by minimizing this maximum delay.

A lower bound on the cycle time is given by the total length of the paths divided by two (since there are two iterations). We obtain

tcycle ³ max (A+E,1/2(D+F+B+E),1/2(B+E+D+F),C+F)

Note that the second and third components of this expression have the same value.

However, this bound cannot be always achieved, because of the restrictions on the placement of registers.

For reduced hardware complexity we restrict the discussion to the two-registers case. We now perform an analysis to obtain the conditions for minimum cycle time. We consider the possibility of partitioning the nodes and placing the register between these partitions. However due to the characteristics of each of the nodes, the partition is not convenient for all of them. The following considerations should be taken into account

• The nodes that can be considered for partitioning should have enough logical depth. In this sense the half adders (nodes A and E) and the decoded (buffered) multiplexers (nodes B and C) seem not suitable for partitioning. Then we only consider the potential partitioning of nodes D (partitions D1 and D2 so that D=D1+D2) and F (F=F1+F2).
• For two registers, since E is not partitioned, the register should be placed after this node (if it is placed before a total of three registers are necessary). Moreover, also for this case, it is not necessary to consider the partition of D, since the registers are placed in nodes E and F.

With these considerations we have the following paths between registers:

1. R1 ® R1: F2+C+F1 = F+C = t_ha+t_SDc+t_nm .
2. R1 ® R2: F2+B+E = F2+t_wm+t_ha .
3. R2 ® R1: D+F1 = 3t_ha+F1 = 3t_ha+F-F2 = 4t_ha+t_SDc-F2 .
4. R2 ® R2: A+E = 2t_ha .

At this point we can discard Path R2 ® R2 as critical, since it is composed only of two half adders. Therefore the problem consists in finding F2 (and then F1 ) so that the maximum of Path R1 ® R1, Path R1 ® R2 and Path R2 ® R1 is minimized. Since Path R1 ® R1 does not depend on F1 nor F2 , we try first to minimize the maximum of Paths R1 ® R2 and R2 ® R1.

Path R1 ® R2 is a increasing function of F2 and Path R2 ® R1 is a decreasing function with the same variable. Therefore the minimum of the maximum of Paths R1 ® R2 and R2 ® R1 is obtained when Path R1 ® R2=Path R2 ® R1. Using this condition we obtain

F2 = 3tha+tSDc-twm 2

and then

Path  R1 ® R2 = Path  R2 ® R1 = 5tha+tSDc+twm 2

Note that F is composed of a half adder and the sign-detector-and-coder and that it is convenient to place the flip-flops so that the half adder is not partitioned. If F2 > t_SDc it might be necessary to place the flip-flops inside the half adder to optimize the path. However this condition is satisfied only if t_SDc+t_wm < 3t_ha which seems not to be true for practical implementations.

The critical path is max(Path  R1 ® R1, Path  R1 ® R2 = Path  R2 ® R1) , that is

tcycle = max æ ç è tha+tSDc+tnm, 5tha+tSDc+twm 2 ö ÷ ø

Note that in case the maximum corresponds to Path R1 ® R1, the placement of registers does not affect the cycle time. In that case, the placement of registers might be guided by the reduction in the number of flip-flops, with the condition max(Path  R1 ® R2,Path  R2 ® R1) £ Path  R1 ® R1 so that the cycle time remains the same.

3.2  Complete algorithm

We now describe the complete algorithm for radix 4 and quotient-digit set {-2,-1,0,1,2}.

3.2.1  Initialization

The standard initial values are w[0] = 2^-2x (to assure w[0] £ (2/3)d) and q[0] = 0. Since this produces 2^-2q, an additional iteration is required. The actual initialization depends on the location of registers (since these have to be initialized). For the two-register case, one possibility is

• w[-1] = 2^-4x

• q₀ = 0 (this requires that the register, which does not contain necessarily the q_j value⁸, should be initialized so that q₀ = 0 is produced).

After this initialization, the first iteration produces w[0] = 2^-2x and q₁ (or the value associated with q₁ in the corresponding register).

3.2.2  Iterations and Termination

To obtain the quotient of n radix-4 digits (including the rounding bit), it is necessary to compute n+1 digits (since, because of the initialization, the algorithm produces 2^-2q). At the end of n+1 iterations, one register contains w[n] and the other register a value ässociated" with q_n+1. After that it is necessary to

• Obtain q_n+1 and the last residual w[n+1] ( one cycle)

• Detect sign of residual, correct quotient, normalize, and round (one cycle).

The total number of cycles is then n+3. This number of cycles is the same as for the other retimed schemes.

4  Estimation and Comparison

In this section we estimate the execution time to obtain a normalized rounded quotient of 53 bits (double precision) using the proposed implementation of the selection function and compare it with previous radix-4 implementations. We also estimate and compare the cell areas.

For this estimate we have used a 0.35 mm standard-cells library with power supply of 3.3 V and Synopsys analysis and synthesis tools (Design Analyzer). We performed the estimation pre-layout, therefore, we do not take into account the additional delay due to the actual parasitic capacitance of interconnections. To make the estimation as independent as possible from the technology we also give the delay using as unit the delay of an inverter loaded with four inverters; we call this unit t_std and it is 0.15 ns. for the library used.

As a first step we perform the timing of the recurrence. To do this, we use the delays of the modules⁹ indicated in Figure 4 and given in Table 3. Using the procedure described in the previous section¹⁰, we determine that the lower-bound of the cycle time (including register setup and propagation delay) is 2.40 ns and the registers should be placed as shown in the diagram of Figure 5.

To have a more reliable estimate we have done a global synthesis of the whole unit. In the synthesis of the part which computes the quotient digit, we lumped the short mux, the two levels of carry-save adders and the upper part of the sign-detector-and-coder (see Figure 3), into one block to optimize logic synthesis across the original blocks boundaries. The resulting cycle time is now 2.42 ns. (see Table 4). The slight increase with respect to the cycle time obtained using the delays of Table 3 is due to the actual loads. In this global implementation we obtained an area of about 4780 nand2 equivalent gates.

Since the proposed algorithm requires (54/2)+3=30 cycles for double precision, the execution time is 73 ns. For the comparison, we synthesized the complete unit using the standard quotient-digit selection function and a variation of [6] using carry-save adders (Figures 2a and 2b). In these cases, the registers store directly w[j] and q_j+1 since there is no advantage in other placements. Again for best use of the synthesis tool we lumped together the modules that compose the quotient-digit selection.

We obtained the cycle times reported in Table 4. From the table we conclude that the proposed implementation produces a speedup of about 1.35 and that the implementation of Figure 2b (variant of [6] using carry-save adders and retimed recurrence) produces a small speedup with respect to the basic implementation. The areas are roughly the same in all schemes.

5  Conclusions

We have developed a scheme to reduce the cycle time of digit-recurrence division by retiming part of the quotient-digit selection so that it is not in the critical path. In addition, this modification allows the placement of the registers in a way to minimize the delay. Although the scheme has been developed for a general radix, all illustrations and evaluations have been done for radix 4. For this radix, we have estimated a speedup of about 35% with respect to the basic implementation and about a 30% with respect to the variation described in [6]. A natural extension would be to develop the details for higher radices.

We have only considered division but, as for the standard implementation, it can be combined with a similar scheme for square root.

References

[1]

M. Ercegovac and T. Lang, "Division and Square Root: Digit-Recurrence Algorithms and Implementations", Kluwer Academic Publishers, 1994.

[2]

T. Fu et al., "R18000: The latest SGI superscalar microprocessor", in Slides of presentations of Hot Chips 13, August 19-21, 2001.

[3]

J. Clouser et al., Ä 600 MHz superscalar floating-point processor", IEEE Journal of Solid-State Circuits, Vol. 32, no 7, pp. 1026-1029, 1999.

[4]

M. Suzuoki, et al., ``A microprocessor with a 128-bit CPU, ten floating-point MAC's, four floating-point dividers, and a MPEG2 decoder'', IEEE Journal of Solid-State Circuits, Vol. 34, no. 11, pp. 1608-1618, 1999.

[5]

G. Hinton, et al. Ä 0.18 um CMOS IA-32 Processor with a 4-GHz Integer execution Unit", IEEE Journal of Solid-State Circuits, Vol. 36, no. 11, pp. 1617-1627, Nov. 2001.

[6]

N. Burgess and C. Hinds, "Design Issues in Radix-4 SRT Square Root and Divide Unit", Proceedings of the 35th Asilomar Conference on Signals, Systems and Computers, Nov. 2001, pp. 1646-1650.

[7]

J.E. Robertson, Ä new class of digital division methods", IRE Transactions on Electronic Computers, vol. 7, no. 3, Sep. 1958, pp. 88-92.

[8]

A. Nannarelli and T. Lang, "Low-Power Divider", IEEE Transactions on Computers, vol. 48, no. 1, Jan. 1999, pp. 2-14.

[9]

E. Antelo, T. Lang, M. Montuschi and A. Nannarelli, ``Fast Radix-4 Retimed Division with Selection by Comparisons'', Internal Report, Dept. Electrical and Computer Eng., University of California at Irvine, USA. (Available at http://www.eng.uci.edu/numlab/archive).

Footnotes:

¹Research of E. Antelo is partially supported by the Xunta de Galicia under project PGIDT99XI20601A and of T. Lang by UC MICRO Grant 01-047.

²This scheme is similar to the use of truncated multiples of the divisor, but the use of selection constants as comparison points gives more flexibility, which is reflected in a somewhat simpler implementation.

³Actually the scheme proposed in [6] was implemented in standard non retimed recurrence.

⁴That is, the set of constants m_k are obtained from the set m_i,k for the value of i corresponding to the actual divisor.

⁵ëa û_t means truncation of a to t fractional bits.

⁶The full adders have been divided into two half adders so as to have a finer granularity in the timing analysis.

⁷We do not include the register delay or set-up times at this point since these do not affect the placement of registers

⁸Because of the placement of registers, as discussed in Section 3.1

⁹These delays have been obtained by loading each module output with four inverters.

¹⁰We consider the two-register case since this achieves the bound of the critical path.