Low Power and Low Leakage Implementation of RNS FIR Filters

Gian Carlo Cardarilli, Andrea Del Re, Alberto Nannarelli^* and Marco Re

Dept. of Electrical Engineering, University of Rome "Tor Vergata", Rome, Italy
^*Dept. of Informatics & Math. Modelling, Technical University of Denmark, Kongens Lyngby, Denmark

Abstract

1  Introduction

The objective of the work described in [1] was the comparison of the power consumption of Finite Impulse Response (FIR) filters implemented in the traditional two's complement system (TCS) and in the Residue Number System (RNS). The work in [1] took into account the dynamic power dissipation, which was by far the dominant portion of the energy consumed a few years ago.

With the technology scaling, and the increased transistor's leakage due to sub-threshold currents, also the static power dissipation starts to play an important role in today's power budgets. Moreover, the increasing smaller CMOS transistors allow the hardware implementation of extra functions that before were executed in software, and the migration of complex system to portable devices. Because of the implementation of digital filters in ultra low power processors, such as the one used in tiny systems with limited available power, it is important the static power due to leakage is characterized and, possibly, reduced.

To have an idea of the impact of the device's leakage on power dissipation, we implemented a multiplier, which is the basic block of a FIR filter, in a 0.18 mm, a 0.12 mm and in a 90 nm library. We used the same timing constraint, the delay of 25 inverters with fanout of 4 (a standard measure of delay across different technologies) in their respective libraries. The results, shown in Table I, indicate that the power dissipation due to leakage P_stat increases both in absolute value and as the percentage of the overall power dissipation P_TOT. By comparing the 0.18 mm and the 90 nm multipliers, we notice that P_TOT has decreased of about 70% (mostly due to the scaling of V_DD), but the static part P_stat has increased 14 times and its contribution to the total 40 times. Moreover, for the 90 nm implementation, if the multiplier is used as often as 1% of the processor usage time the static power dissipation becomes dominant. Therefore, the design of systems in nanometer technologies must take into account methodologies to reduce the static power dissipation.

In this work, we show that filters implemented in RNS, not only are convenient in terms of dynamic power dissipation (at the same operation rate), but also that the RNS is very effective in the reduction of the static power. In implementing these low power units, we take advantage of state-of-the-art design automation tools [2] which handle libraries of standard cells with dual threshold transistors [3].

2  Background

The use of alternative number systems in the implementation of application specific Digital Signal Processing (DSP) systems has gained a remarkable importance in recent years because of the lower power consumption over their two's complement counterparts.

2.1  Background on Residue Number System

A Residue Number System (RNS) is defined by a set of relatively prime integers

{m1, m2, ¼, mP }  .

The dynamic range of the system is given by the product of all the moduli m_i:

M = m1 ·m2 ·¼·mP .

Any integer X Î [ 0, M-1 ] has a unique RNS representation given by:

X RNS ®   ( áX ñm1, áX ñm2, ¼, áX ñmP )

(1)

where

áX ñmi = X  mod  mi        (  e.g.   X = ami + áX ñmi   )

A comprehensive description of the RNS theory and its application to computer systems can be found in [4], [5] and [6].

In the RNS base, operations, such as addition and multiplication, are done in parallel on the moduli

Z = X op Y   RNS ®      ì ï ï ï í ï ï ï î Zm1 = áXm1 op Ym1 ñm1 Zm2 = áXm2 op Ym2 ñm2 ¼           ¼           ¼ ZmP = áXmP op YmP ñmP

(2)

The conversion of the RNS representation of Z can be accomplished by the Chinese Remainder Theorem (CRT):

Z = P å i = 1    mi   ·á mi    -1   ñmi ·Zmi  M

(3)

with [`(m<sub>i</sub>)] = [M/(m<sub>i</sub>)] and [`(m_i)] ^-1 obtained by á[`(m<sub>i</sub>)] ·[`(m_i)] ^-1 ñ_mi = 1.

Clearly, the conversions from N to RNS, and vice-versa, constitute a significant overhead in systems implemented in RNS. However, efficient methods to perform those conversions are presented in [7], [8], and [9].

2.2  Implementation of FIR Filters in RNS

A FIR filter of order N is described by the expression

y(n) = N å k = 1  ak x(n-k)

(4)

and it can be realized in transposed form as shown in Figure 1.

As a direct consequence of (2), expression (4) becomes in RNS:

y(n) = N å k = 1  ak x(n-k)         RNS ®

(5)

ì ï ï ï ï ï ï í ï ï ï ï ï ï î Ym1(n) = N å k = 1   áAm1(k) ·Xm1(n-k) ñm1 m1  Ym2(n) = N å k = 1   áAm2(k) ·Xm2(n-k) ñm2 m2  ¼           ¼           ¼ YmP(n) = N å k = 1   áAmP(k) ·XmP(n-k) ñmP mP

and the filter can be implemented in RNS by decomposing it into P FIR filters working in parallel, as sketched in Figure 2.

3  Cell library and power dissipation

The standard cell library used provides two classes of cells: cells with devices with a reduced threshold voltage (V_t) designed to achieve high speed, identified in the following as HS, and cells with devices with a higher V_t to provide low leakage identified as LL [3].

Moreover, we consider the cells operating at the typical case conditions with a power supply V_DD = 1.0 V and a temperature of 25 C.

By comparing the data-book for the two classes of cells HS and LL, the following points emerge when comparing the same cell (e.g. a NOT gate):

• The HS cell is faster than the corresponding LL cell. For the 1X drive NOT gate loaded with 4 SL (library standard load) the HS gate is about 30% faster than the LL one.
• The area is the same.
• The input capacitance is slightly smaller for the LL cells: For the 1X drive NOT gate, the input capacitance in the LL cell is 10% smaller than in the HS cell.

The total power dissipation for a CMOS gate is

PTOT = Pload + Psc + Pleak

(6)

The term P_load is the power dissipated for charging and discharging the capacitive load C_L when the output toggles at a rate f_p [10]

Pload = CL VDD2 fp  .

(7)

Therefore, HS and LL cells loaded with the same C_L and with the same switching activity consumes the same P_load. However, for clusters of cells of the same type (due to the reduced input capacitance) the LL cells show a lower P_load, if the activity is the same. For a chain of inverters toggling at the same rate, the HS cells dissipate about 5% more than the LL cells.

The power due to short circuit currents P_sc is

Psc = b 12 ( VDD - 2 Vt )3  trf tp

(8)

where b_HS ³ b_LL, t_rf is the average rise and fall time and t_p = 1/f_p [10]. From (8), it is clear that for the LL cells P_sc is lower than for HS cells, although, due to the longer transition times, the term t_rf is higher.

The term P_leak is the static power dissipation

Pleak = VDD Isat

(9)

where I_sat is the reverse saturation current. This contribution is independent of the switching activity, but depends on the state (logic level of the inputs) of the gate. The LL cells are designed to have a P_leak several times smaller than the corresponding HS cells.

In summary, LL cells are slower than HS cells, but dissipate less dynamic (if the switching activity is the same) and static power than the corresponding HS cells.

The current version of Synopsys Design Compiler [2] can handle the synthesis of dual V_t standard cell libraries such as the one described above. The prioritized design constraint is the delay (or better the clock period for a synchronous sequential system), but the tool keeps the power dissipation down by substituting HS cells with LL when there is a sufficient time slack. Moreover, the dynamic power dissipation is optimized as indicated in [11].

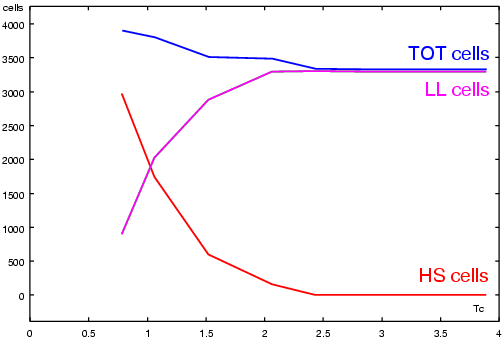
Figure 3 shows the variations in the HS and LL cell mix for a system synthesized with different values of the timing constraint T_C. In the circuit synthesized with the smallest T_C (minimum delay), the number of HS cells is dominant over the LL cells. For the circuit synthesized with a longer T_C (right side of Figure 3), all cells are of LL type to have a reduced power dissipation.

4  Low power FIR filters

The objective of the work is the reduction of the overall power dissipation without affecting the throughput of the filter, and to evaluate which of the techniques used for the reduction of the dynamic power dissipation are also beneficial for the static part.

Because each logic function can be implemented with a HS or a LL cell, the first idea is to replace faster and power hungrier HS with LL cells when possible. By the RNS decomposition of Figure 2, the filter is divided into as many independent clusters of cells as the RNS moduli. Because of the different size of the moduli, the clusters have different maximum delays. The available time slack in the faster clusters (smaller moduli) allows to exchange HS with LL cells and reduce both the dynamic and static power dissipation. This is similar to what is done in [12] in the dual voltage approach.

In order to compare the power dissipation of the filters, we have implemented a 16, 32 and 64-tap error-free programmable FIR filter (20 bits dynamic range, transposed form) in the traditional two's complement system (TCS) and in RNS.

Because FIR filters in transposed form are modular with respect to the number of taps (i.e. adding extra taps does not alter the filter architecture), for all the filters, we set as the main design constraint the same maximum delay (i.e. the critical path) which determines the filter's throughput.

The composing blocks of a FIR filter are multipliers, adders and registers. In the following, we describe the architectures chosen for implementing these composing blocks.

4.1  TCS FIR Filters

For the implementation of multipliers with the traditional binary system (TCS), we chose to keep the product in carry-save (CS) format in order to speed-up the operation, and delayed the assimilation of the CS representation to the last stage of the filter. For the FIR filter in transposed form (Figure 1), in each tap we need to add the CS representation of the product to the value stored in the register (previous tap). Again, to avoid the propagation of the carry, we can store the CS representation. For this reason, we need to implement the addition with an array of 4:2 carry-save adders (CSA), as shown in Figure 4.

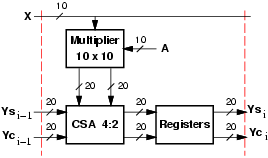The CS representation is finally converted into the two's complement representation by a carry-propagate adder (realized with a carry-look-ahead scheme) in the last stage of the filter.

Figure 4 shows the implementation of the tap of a filter with programmable coefficients.

The critical path is

tTCS = tMULT + tCSA4:2 + tREG

and the expression for the total power dissipation as a function of the number of taps, or filter order, is

PTCS = PTCStap ·N + PCPA

(10)

where P_CPA is the power dissipated by the final carry-propagate adder. Note that the term P_TCStap is the average power dissipated in the taps, and strongly depends on the switching activity and consequently on the value of the coefficients.

4.2  RNS FIR Filters

As already mentioned, a RNS filter can be decomposed, as shown in Figure 2, into P filters of smaller dynamic range (P is the number of moduli) working in parallel.

A key point in the design of the RNS filter is the choice of moduli. To choose the set of co-prime numbers which cover the dynamic range of 20 bits, we used the tool described in [13], which selects the set of moduli giving the best delay/area/power tradeoffs according to the results of the characterization of the RNS filter composing blocks. Based on the tool, we chose for our RNS filters the following set of moduli

{ 7, 11, 13, 17, 64 }

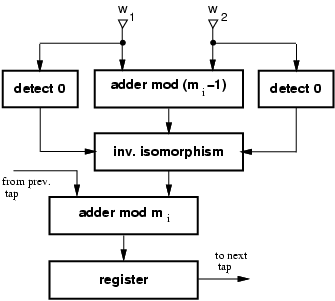
In each tap, a modular multiplier is needed and because of the complexity of modular multiplication, we used the isomorphism technique to implement the product of residues for prime moduli [4]. By using isomorphisms, the product of the two residues is transformed into the sum of their indices which are obtained by an isomorphic transformation (see [12] for implementation detail). The modular multiplication on m_i = 64 is obtained by the normal binary multiplication limited to the 5 least-significant bits.

Figure 5 shows the implementation of a tap for a generic RNS prime modulus. The critical path for RNS filters in transposed form is the maximum delay in the tap for the slowest modulus

tRNS = tmodMULT + tmodADD + tREG

that, for the implementation of Figure 5, is

tRNS = tISO + 2 ·tmodADD + tREG

(see [12] for implementation detail).

The RNS FIR filter is completed by an input and an output conversion block.

Similarly to the TCS, the power dissipation in the RNS filter can be expressed as a function of the filter order

PRNS = PRNStap ·N + Pconv

(11)

where P_conv is the power dissipated by the input and output converters, and the term P_RNStap is the average power dissipated in the taps.

4.3  Results of implementations

The comparison is carried out on filters implemented in the 90 nm STM library of standard cells (V_DD = 1.0 V, at 25 C) [3], and the power dissipation has been computed by Synopsys Power Analyzer based on the annotated switching activity of random generated inputs. All the filters can be clocked at f_max = 500 MHz. Table II (upper part) summarizes the results for the implemented filters. The power dissipation is computed at a clock frequency of 100 MHz.

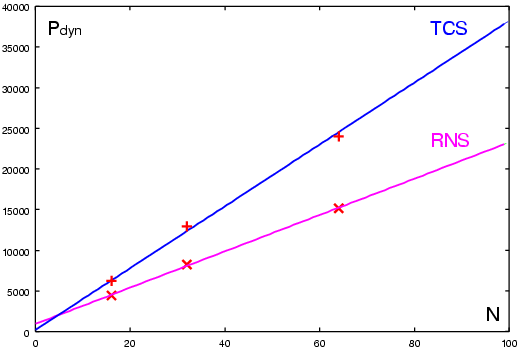
By interpolating the results for static, dynamic and total power dissipation, we obtain expressions of the power as a function of the filter order N (Table II, lower part) similar to those of (10) and (11). These trends are also plotted in Figure 6. The slopes [P/tap] indicated in Table II (lower part) represent the average power dissipated per tap.

From these results, it is clear that the RNS decomposition in parallel paths allows a reduction per tap of 40% for the dynamic and 50% for the static power without delay penalty (throughput). The area of the RNS filters is reduced as well.

5  Conclusions

As the CMOS technology scales, a larger number of devices is integrated on a single chip, but the device's leakage has increased to a limit such that static power dissipation is no longer negligible.

In this work, we take advantage of the properties of the Residue Number System (RNS) to implement FIR filters with reduced static and dynamic power consumption.

The RNS decomposition in parallel paths allows an efficient use of libraries with HS cells, designed for high-speed, and LL cells, designed for low-power. In all the non-critical paths, the available time slack is used to substitute HS with LL cells resulting in a reduction of the power dissipation.

The implementation results show that the RNS filters offer a reduction of 50% in static power dissipation and a total power reduction of 40% with respect to the corresponding conventional filters.

References

[1]

A. Nannarelli, M. Re, and G. C. Cardarilli, ``Tradeoffs between Residue Number System and Traditional FIR Filters,'' Proc. of IEEE International Symposium on Circuits and Systems, vol. II, pp. 305-308, May 2001.

[2]

Synopsys Inc. Synopsys products: Design Compiler. [Online]. Available: http://www.synopsys.com/products/logic/design_compiler.html

[3]

STMicroelectronics. 90nm CMOS090 Design Platform. [Online]. Available: http://www.st.com/stonline/prodpres/dedicate/soc/asic/90plat.htm

[4]

I. Vinogradov, An Introduction to the Theory of Numbers.    New York: Pergamon Press, 1955.

[5]

N. Szabo and R. Tanaka, Residue Arithmetic and its Applications in Computer Technology.    New York: McGraw-Hill, 1967.

[6]

M. Sodestrand, W. Jenkins, G. A. Jullien, and F. J. Taylor, Residue Number System Arithmetic: Modern Applications in Digital Signal Processing.    New York: IEEE Press, 1986.

[7]

T. V. Vu, ``Efficient implementation of the chinese remainder theorem for sign detection and residue decoding,'' IEEE Trans. Circuits Systems-I, vol. 45, pp. 667-669, June 1985.

[8]

S.Piestrak, ``A high-speed realization of a residue to binary number system converter,'' IEEE Trans. Circuits Systems-II Analog and Digital Signal Processing, vol. 42, pp. 661-663, Oct. 1995.

[9]

G. Cardarilli, M. Re, and R. Lojacono, ``A residue to binary conversion algorithm for signed numbers,'' European Conference on Circuit Theory and Design (ECCTD'97), vol. 3, pp. 1456-1459, 1997.

[10]

N. H. E. Weste and K. Eshraghian, Principles of CMOS VLSI Design, 2nd ed.    Addison-Wesley Publishing Company, 1993.

[11]

B. Chen and I. Nedelchev, ``Power compiler: A gate-level power optimization and synthesys system,'' Proc. of International Conference on Computer Design (ICCD), pp. 74-78, Oct. 1997.

[12]

G. C. Cardarilli, A. Nannarelli, and M. Re, ``Reducing power dissipation in FIR filters using the residue number system,'' to appear in Proc. of the 43rd IEEE Midwest Symposium on Circuits and Systems, Aug. 2000, available at http://dspvlsi.uniroma2.it/pubs/mwscas00/.

[13]

A. Del Re, A. Nannarelli, and M. Re, ``A tool for automatic generation of RTL-level VHDL description of RNS FIR filters,'' Proc. of 2004 Design, Automation and Test in Europe Conference (DATE), vol. 48, pp. 686-687, Feb. 2004.