|
Copyright 2000 IEEE. Published in the Proceedings of 34th Asilomar Conference on Signals, Systems, and Computers, pages 879-883, Asilomar Hotel and Conference Grounds, Pacific Grove, CA, USA. Oct. 29 - Nov. 1, 2000.
The new generation of telecommunication equipment often require the use of high order FIR filters for the implementation of the new modulation schemes. Moreover, low power consumption for new portable multimedia terminals is needed. In this context, computational intensive signal processing blocks can be effectively implemented by using Residue Number System (RNS) arithmetic.
The use of the RNS allows the decomposition of a given dynamic range in slices of smaller range on which the computation can be efficiently implemented in parallel [1], [2], [3]. The QRNS (Quadratic RNS) is particularly convenient when dealing with complex numbers [4] [5]. In QRNS the imaginary term of a complex number is transformed into an integer, therefore a complex multiplication which requires four integers multiplications and two sums in the conventional two's complement system, is implemented with two integer multiplications in QRNS.
The drawback presented by the RNS (and QRNS) is the overhead due to both input and output conversions binary-RNS-binary. This problem can be solved by using efficient conversion techniques [6] [7], or by converting directly the analog signal in the residue representation [8].
Recently, a number of works on low power and RNS have been presented. In [9] and [10] the power dissipation is reduced by taking advantage of the speed-up due to the parallelism of the RNS structure. The supply voltage is reduced, resulting in a quadratic reduction of power, until the speed-up = 1 [9], or until the desired value of delay [10]. In [11] some encoding optimization techniques for small moduli are presented.
In our work, we compare the performance, area and power of a complex FIR filter realized with the traditional binary arithmetic, with a QRNS based one.
Both filters have been designed according to the specifications of an actual filter used in a telecommunication satellite and are clocked at the same rate of 166 MHz. Although the QRNS filter has a longer latency, it can sustain the same throughput of the traditional one, while its area and power dissipation are about 57% of the total area and 34% of the total power of the traditional filter.
A Residue Number System is defined by a set of relatively prime integers
|
|
|
|
|
In the complex case, we can transform
the imaginary term into an integer if the equation q2+1 = 0 has
two distinct roots q1 and q2 in the ring of integers modulo mi
(Zmi).
A complex number xR + j xI = (xR, xI) Î Zmi, with q
root of q2+1 = 0 in Zmi has a unique Quadratic Residue
Number System representation given by
|
|
|
Moreover, it can be proved that for all the prime integers which satisfy
|
As a consequence, the product of two complex numbers xR + j xI
and yR + j yI is in QRNS
|
| ||||||||||||||||||||||
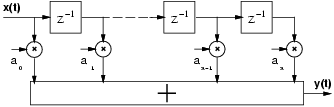
A complex N taps FIR filter (Figure 1) is expressed by
|
 |
 |
The starting point of our design is a programmable 64-tap FIR filter realized in direct form (Figure 1) with complex input and coefficients size of 10 bits for the real part and 10 bits for the imaginary part. These data are derived from the specification of an actual digital filter, used aboard a satellite for direct TV broadcasting. We designed a prototype filter in traditional two's complement system in order to compare its performance, area and power dissipation with a QRNS filter.
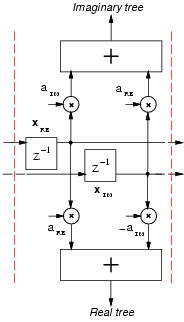
The filter can be decomposed in a real and imaginary part. A single tap is realized as sketched in Figure 3. The real and imaginary products are realized with two Booth multipliers [12] and the resulting partial products are accumulated in a Wallace's tree structure which produces a carry-save (CS) representation of the product in each side of the filter. The CS representation of the products, is then accumulated in two 128-addend Wallace's tree realized with 4:2 compressors [13], not depicted in Figure 3. To have an error-free filter we must keep a number of bits sufficient to hold the carry-save representation of the sum, and we need a 20 + log2 64 wide tree. The carry-save representation is finally converted into two's complement representation by a carry-propagate adder (realized with a carry-look-ahead scheme) in the last stage of the filter (both real and imaginary sides).
The filter has been implemented in the AMS 0.35 mm standard cells library, and it was synthesized from VHDL description using Synopsys and a constraint of 6 ns as a critical path, for this reason it resulted in a pipelined filter of 6 stages.
 |
From Figure 2 we can see that the QRNS filter can be realized
by two RNS filters in parallel.
Each RNS filter is then
decomposed into P filters working in parallel, where P is the number of
moduli used in the RNS representation. In addition, the RNS filter requires
both binary to QRNS and QRNS to binary converters. In order to have a
dynamic range of 20 bits, as in the case of the traditional implementation,
we chose the following set of moduli:
|
|
In each tap, a modular multiplier is needed to compute the term
áak x(n-k)ñmi.
Because of the complexity of modular multiplication, we used the
isomorphism technique [14] to implement the product of
residues.
By using isomorphism, the product of the two residues is transformed
into the sum of their indices which are obtained by an isomorphic
transformation.
According to [14], if m is prime there exists a primitive
radix r such that its powers modulo m
cover the set [1, m-1]:
|
|
|
For example, for the modular multiplication
|
|
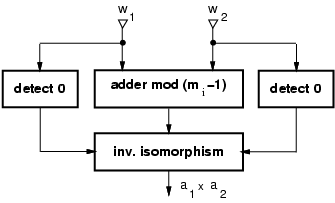
The input x, although delayed, is the multiplicand of all the multiplications (see Figure 1). For this reason only one isomorphic transformation, incorporated in the binary to QRNS conversion, is necessary for all the taps. On the other hand, because the coefficients of the filter (multiplicators) are constant terms loaded once at start-up, it is convenient to load directly the isomorphic representation modulo mi-1. As a result, in each tap, we reduce the modular multiplication to a modular addition followed by an access to table (inverse isomorphism) as depicted in Figure 4. The table is implemented as synthesized logic and special attention has to be paid when one of the two operands is zero. In this case, there exists no isomorphic correspondence and the modular adder has to be bypassed.
 |
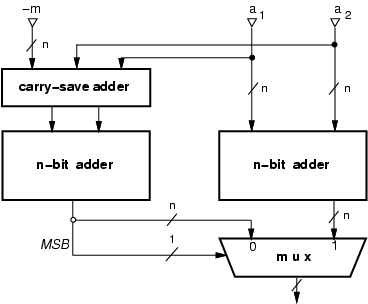
The modular addition
áa1 + a2 ñm,
consists of two binary additions. If the result
of a1 + a2 exceeds the modulo (it is larger than m-1),
we have to subtract the modulo m. In order to speed-up the operation
we can execute in parallel the two operations:
|
 |
At the output of the tree, it is necessary to reduce the sum S of all the taps to áS ñmi . This is done with the modulo-reduction technique described in [6].
As already mentioned, the input conversion block includes the isomorphic transformation. If x is zero, there is no exponent w such that árw ñmi = 0. As a consequence, zero is encoded with a special pattern that is then detected in the block which computes the product using the isomorphism (Figure 4).
The output conversion is implemented by using the Chinese Remainder Theorem (CRT), as described in [6].
Both the traditional and the QRNS filters were implemented in the AMS 0.35 mm standard cells library. Delay, area and power dissipation have been determined with Synopsys tools.
Table 2 summarizes the results. In the table, area is reported as number of NAND2 equivalent gates and power is computed at 166 MHz. However, both area and power dissipation do not take into account the contribution of interconnections.
Table 2 shows that the QRNS filter has a higher latency, due to the conversions, but it can be clocked at the same rate of the traditional filter, and consequently, it can sustain the same throughput. However, the QRNS filter is almost half the area on the traditional complex filter, and consumes one third of the energy.
| ||||||||||||||||||||||||||||||
We have implemented a QRNS 64-taps FIR filter and compared its delay, area and power dissipation with those of a corresponding complex FIR filter realized with the traditional two's complement system. The results obtained show that the QRNS filter can sustain the same clock rate, although it has a slightly longer latency. However, in terms of area and power the QRNS version is more convenient. A better improvement is expected for filters with a larger number of taps.
134th Asilomar Conference on Signals, Systems, and Computers, Asilomar Hotel and Conference Grounds, Pacific Grove, CA, USA. Oct. 29 - Nov. 1, 2000.