Copyright 2004 IEEE. Published in the Proceedings of Design, Automation and Test in Europe Conference (DATE) Vol. 48, p. 686-687, Paris (France), Feb. 16-20, 2004.

A Tool for Automatic Generation of RTL-Level VHDL Description of RNS FIR Filters

A. Del Re, A. Nannarelli^* and M. Re
Dept. of Electrical Engineering, Univ. of Rome "Tor Vergata", Italy
^* Informatics & Mathematical Modeling, Technical University, Denmark

Abstract

1  Introduction

A Residue Number System (RNS) is defined by a set of relatively prime integers {m₁, m₂, ¼, m_P } . Its dynamic range is given by the product M = m₁ ·m₂ ·¼·m_P . Any integer X Î { 0, 1, 2, ¼M-1} has a unique RNS representation given by:

X RNS ®   ( áX ñm1, áX ñm2, ¼, áX ñmP )

where áX ñ_mi denotes the operation X mod m_i [1]. Operations on different m_i (moduli) are done in parallel

Z = X op Y   RNS ®      ì ï ï ï í ï ï ï î Zm1 = áXm1 op Ym1 ñm1 Zm2 = áXm2 op Ym2 ñm2 ¼       ¼       ¼ ZmP = áXmP op YmP ñmP

As a consequence, operations performed on large wordlengths can be split into several modular operations executed in parallel and with reduced wordlength.

Although, previous work showed that the application of RNS to FIR filters leads to faster designs and reduced power dissipation with respect to the traditional filter implementation in the two's complement system [2], the RNS is not very popular because of the more complicated algorithms involved for conversions and modular operations.

In this work, we introduce a tool that hides the RNS algorithms and provides the designer with an interface in which the usual filter parameters and design constraints (timing, area, power) only appear.

The tool can design both programmable and constant coefficients FIR filters in transposed form. Moreover, the tool chooses the set of RNS moduli which cover the given dynamic range and best fit the design constraints. The design space exploration is based upon a characterization of the blocks composing the filter, and it is done for the different technologies supported: standard cells and FPGAs.

Differently from the tool for RNS design presented in [3], we only target FIR filters but offer a wide range of design choices and an automatic selection of the set of moduli which best fit the design constraints.

The tool is suitable for an IP oriented design of System-on-Chips offering to the designer the performances of RNS, but completely hiding its complexity.

2  Tool Description

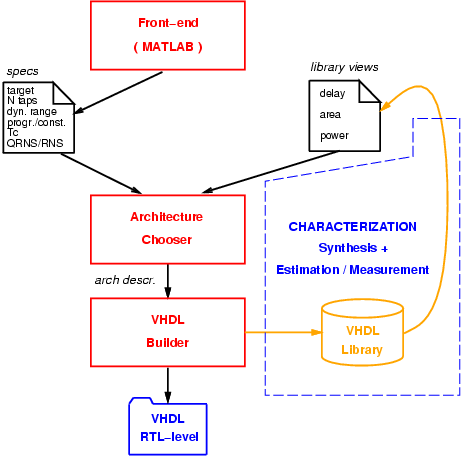
The structure of the tool is shown in Figure 1. It is divided into three main blocks:

A front-end which generates a list of parameters specifying the filter characteristics such as: dynamic range (i.e. wordlength), filter order, etc.. The front-end could be a commercial tool, such as MATLAB.

Architecture Chooser (AC) chooses the filter architecture, selected among a set of supported ones, that minimizes a given cost function. The selection is done according to the filter parameters passed by the front-end, the target technology library specifications, and the design constraints. Moreover, AC generates a set of instructions describing the detail of the selected architecture to be passed to the builder.

VHDL Builder (VB) generates the VHDL descriptions of the elementary blocks (modular multipliers and adders, converters, ¼ ), and the top-level filter netlist. Moreover, it builds a VHDL test bench file to verify the filter functionality (e.g. to check if the VHDL simulations match the MATLAB fixed point simulation results), and a synthesis script for the synthesizer (only Synopsys Design Compiler is supported at this time).

The Architecture Chooser (AC), according to the project constraints and the library views (timing, area and power), determines the set of RNS moduli to be used, the architectures used in each RNS path, and the overall filter organization (RNS paths plus converters [2]). Currently, AC supports a number of optimization directives such as: filter with minimum area or lower power dissipation for a given clock period (T_C), filter with minimum area or lower power dissipation at any T_C. Moreover, The AC instructs the VHDL Builder, to place pipeline registers, if necessary.

3  Characterization

The characterization of the basic blocks composing the filter is the key for an accurate estimate of the cost function. Therefore, the outcome of AC depends on an accurate characterization. For each RNS modulus (currently we consider a set of about 30) all basic blocks must be characterized in terms of timing, area and power. Furthermore, because we provide RTL-level descriptions to the synthesizer, the area (and the power dissipation) largely depends on timing constraints. As a consequence, the area and power characterization of a block must be done for different clock rates, increasing the complexity of the cost function to minimize. For the characterization of the power dissipation, we assume random activity at the blocks input. To make the tool as independent as possible of the library, as an option in AC, we can use standard units for (delay, area, and power)¹. In this way, when changing technology, the characterization process is reduced to a few runs. We use the VHDL Builder to generate all blocks to be characterized (Figure 1).

4  Examples and Results

To test the accuracy of the estimates and, consequently, the soundness of the architectural choices made, we generated with the tool a number of FIR filters varying the dynamic range (dyn), the filter order (N), and the timing constraints (T_C). The target technology is the STM 0.35 mm standard cell library. In Table 1, we report the area estimates (as NAND2 equiv.) and the corresponding actual values determined after synthesis performed by Synopsys Design Compiler. From the last column of the table, the estimate error is less than 10% on the average.

5  Conclusions and Future Work

In this work, we presented a tool which generates a synthesizable VHDL description of RNS FIR filters completely hiding the RNS algorithms and details to the filter designer. The results of the synthesis of the automatically generated RNS filters show differences of less than 10% with respect to the initial estimation, making the tool suitable for design exploration at an early stage of the project.

The tool is still under development and open to the inclusion of more architectural choices and optimization criteria.

References

[1]

M.A. Sodestrand et al., Residue Number System Arithmetic: Modern Applications in Digital Signal Processing, New York, IEEE Press, 1986.

[2]

A. Nannarelli, M. Re, and G. C. Cardarilli, ``Tradeoffs between Residue Number System and Traditional FIR Filters,'' Proc. of IEEE International Symposium on Circuits and Systems, vol. II, pp. 305-308, May 2001.

[3]

D. Soudris et al., ``A methodology for implementing FIR filters and CAD tool development for designing RNS-based systems,'' Proc. of IEEE Int.l Sym. on Circuits and Systems, vol. V, pp. 129-132, May 2003.

Footnotes:

¹The delay of a NOT gate with fan-out=4, the area of a NAND2 gate, and the power dissipated by a NOT with fan-out=1 at 100 MHz.