About the HD-Tomo Tomography Project

About the HD-Tomo Project
High-Definition Tomography
Tomography is the science of "seeing through objects." Physical signals
- waves, particles, currents - are sent through an object from many
different angles, the response of the object to the signal is measured,
and an image of the object's interior is reconstructed by means of
a computer.
Tomography is behind some of the most important and profound scientific
discoveries of all times: The interior structure and processes of the Earth,
Moon and Sun and the first maps showing the location of simple mental
processes in the human brain are notable examples.
The Goal
A decisive factor behind the human brain's unrivalled success with 3D
reconstruction is the ability to use prior information - an organized
accumulation of experience with similar objects.
The goal of the HD-Tomo project is to accomplish this on a computer:
We use state-of-the-art mathematics and scientific computing to develop
the enabling technology for next-generation tomographic reconstruction
algorithms that can incorporate a variety of prior information, and thus
achieve major improvements in the details and reliability of
high-definition reconstructions - sharper images with reliable details.
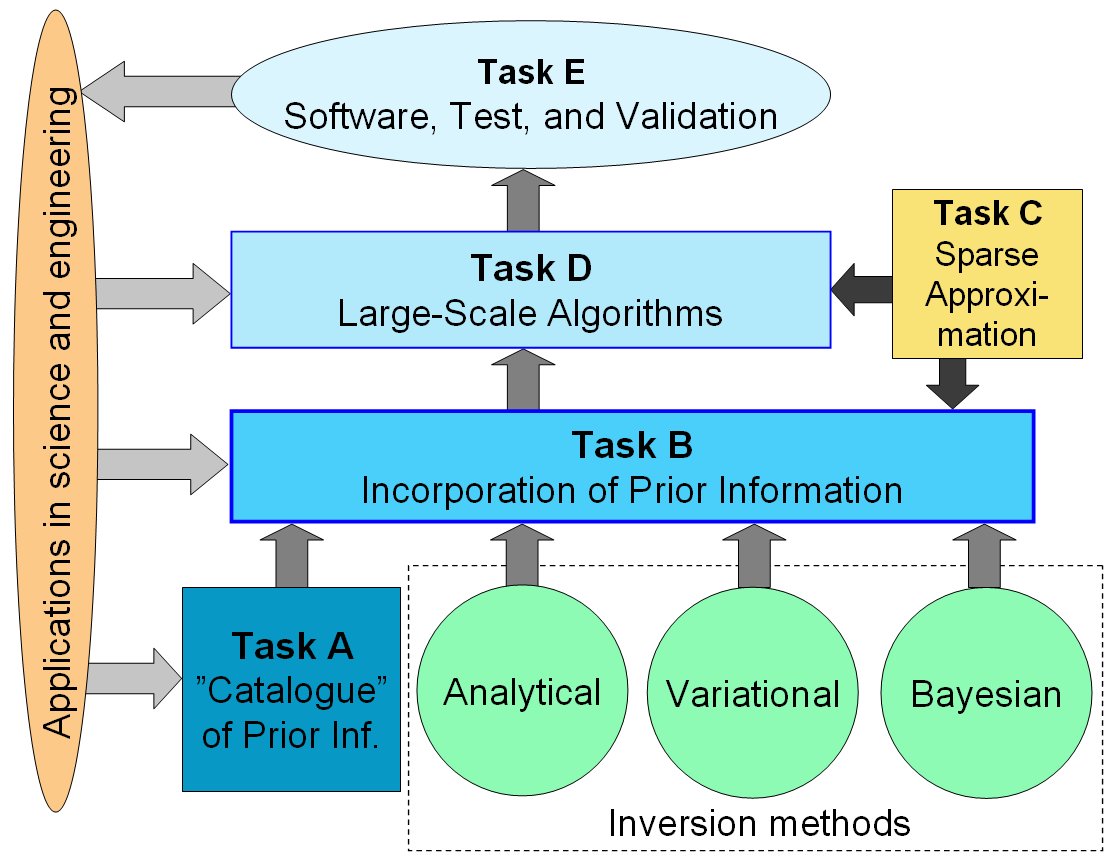
The Challenges
Prior information comes in many different forms (e.g., constraints,
statistical priors, or "catalogues" of trustful images) and the challenge
is to design new mathematical methods that incorporate all this
information in an optimal way. An additional challenge is how to
represent and perform computations with the huge amounts of data in
3D reconstructions.
The Ingredients
We will consider a variety of problems, based on both linear and nonlinear
models, and using integral equations as well as partial differential
equations. We will also consider a variety of reconstruction methods,
including analytical inversion methods, methods based on a variational
formulation, and sampling methods in a Bayesian formulation.
To incorporate all available prior information in various forms, we will
replace classical algorithms built on ad-hoc assumptions with new
algorithms based on models and methods that take their basis in the
actual prior information in a given problem.
The Focus
We focus on development of mathematical and numerical algorithms in
an applied mathematics research environment that has close ties
to information technology and high-performance computing, and the
research will incorporate close collaborations with scientific and
industrial users of tomography. Our computational methods must be
targeted to a range of computational platforms including personal
computers and small-scale clusters that are standard equipment in
labs today. To ensure the dissemination of our results outside the
applied mathematics community we will also publish joint papers
with the application experts.
The Impact
By means of our new methods, scientists/engineers will be able to
advance the use of tomographic methods in a wide range of applications:
Our research will have impact on, e.g., security scanners for passengers
and cargo, oil/gas/geothermal energy exploration, process and production
monitoring for safety and quality, X-ray and neutron scattering in
materials science, and medical applications such as dementia diagnostics,
screening, and surgery aid. But our results are not restricted to
tomography - rather, we expect that our results will have a broader
impact on the general field of applied and computational mathematics
relating to imaging problems.
For more information, see the pdf file with the
project presentation slides.