What Is a Computer?

Andreas Bærentzen (ver. 3.12, July 2024)

Prompt to Diffusion Bee:
"powerful computer in the style of Lichtenstein"

Books on computer programming do not, in general, contain a primer on the principles of how computers work. That is not surprising since this is a big topic in its own right. An aspiring programmer who began by studying how computers work at the hardware level - before learning any programming languages - would likely be confused rather than aided by being so thorough. On the other hand, programmers do need a mental model of what happens when a program executes. Without such a mental model, it is easy to introduce bugs, write hard-to-maintain code, or simply create very slow programs.

The aim of this document is to provide just the right amount of knowledge about how a computer works to be useful to programmers without getting lost in hardware details that may be interesting in their own right but do not help programmers. We approach this challenge by introducing a model computer which we will call the Super Simple Model Computer (SSMC). The SSMC is a high level model consisting of a processor and memory, and we will simply describe what instructions are understood by the processor, how memory is accessed, and the general flow of execution. At this level of explanation, we can ignore things like binary numbers, logic gates, clock frequencies, and the list goes on. In fact, the model is completely independent of what technology we might choose to realize the computer. Nevertheless, a realization of the SSMC could be built. We know this because we can make a physical computer pretend to be the SSMC and simulate the execution of programs that are written for the SSMC.

Thus, in essence, this document is a whitepaper for a computer that does not exist but which could be constructed if someone made all the necessary decisions about how to put the hardware together. Our belief is that this is precisely the level at which it is most important for programmers to understand computers. Of course, some programmers write programs that do require an understanding of the physical hardware, and we refer to Petzold's book [1] as a place to embark on that journey. For the rest of us, the SSMC may be simple, but anything that is computable could be computed by the SSMC and it is not even too different from a real computer at the level at which we describe it. This is why we believe it is a useful tool for developing a mental model. Essentially, if a reader has understood the SSMC they also know approximately what happens when their programs run on a real computer.

What is shown below is a simulator that runs an SSMC program.

The program computes powers of 2 and stops when it reaches 1024. For the time being this simulation may seem a little mysterious, and if you are wondering about the little arrow, it simply points to the instruction currently being executed, and in the following all the rest will be explained.

The SSMC itself is described in Section 1. In Section 2, we discuss some elements of computer science that build on the SSMC. This section provides information that is perhaps of even more immediate use to programmers than Section 1. Admittedly, Section 2 might also be a bit less accessible, and perhaps it is most useful to people after they have learnt basic programming. Section 3 goes on to address the question of what is computable. Probably, this is not essential for most readers, but this is where we show that the SSMC can compute anything that is computable. In Section 4, we discuss how the SSMC compares to real world computers - early ones in particular. This brief section is mostly for historical context.

1. The Super Simple Model Computer

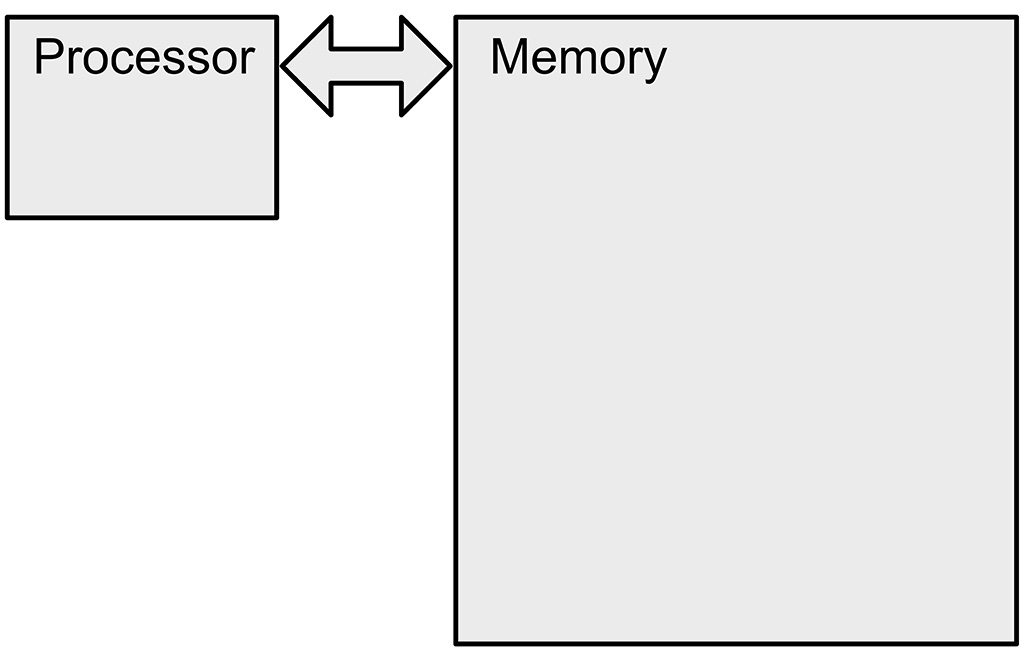
At the highest level of abstraction, the SSMC (along with any other computer) consists of a central processing unit (CPU) and random access memory (RAM). In the following, we will refer to these two entities simply as the processor and the memory. The main goal of this text is to explain in very broad terms what these two things are and how they work together.

The figure below shows the relationship between processor and memory. At the most abstract level, the processor reads instructions and data from memory, executes the instructions, and then writes output back to memory. The "execution of the instructions" is where the computation happens.

The Memory

The terminology is a little confusing when it comes to computer memory. Some would argue storage is a better word than memory since a computer does not remember in the human sense. On the other hand, the type of memory that is used in modern computers is Random Access Memory, or simply RAM, and since memory is part of that name, we will stick to that. Also, the word storage is broader and used, for instance, in "disk storage" and "tape storage".

We can think of computer memory as a list of cells, each of which may contain either a number or an instruction encoded as a number. Admittedly, the instructions might take up more space than a single number, but that is a detail which we will cheerfully ignore. However, it is very important that the cells are numbered and that we can access any cell in the memory simply by specifying its number. It is also important that it is equally fast to access any cell in the memory. In fact, that is the whole point of "random access", and it can be seen as the opposite of a storage system where you have to read through all of the preceding memory cells in order to get to the one you want.

It may be helpful to think of memory cells as the cells of a spreadsheet for readers who are familiar with spreadsheets such as Microsoft Excel. In a spreadsheet, we can also access a cell by specifying its row and column number, and each cell can contain either an instruction, a number, or something else. An even simpler way to understand computer memory is that each cell is like a box with a number on it. This number serves as a label and ensures that the processor can always find the box and either read the information inside it or replace it with new information.

Short-Term Memory

In addition to the ordinary memory, which is outside of the processor, the processor also has a "short-term" memory. We identify cells in the short-term memory by letters, but otherwise they are similar to those of the long-term memory. We will assume that the SSMC has nine short-term cells labelled a, b, c, i, j, k, x, y, and z. We could make do with less, but it turns out to be convenient to have a generous amount of short-term memory.

To simplify things a bit, all computations are performed on the short-term memory in our SSMC, but since most of the data is going to be in the ordinary memory, we need a way to transfer from long-term to short-term and also the other way. Transferring between the two types of memory is done by the processor, and we will discuss the instructions for this in the next section.

The Processor

Like any microprocessor, the SSMC processor simply works its way through the cells of the long-term memory (i.e. RAM) executing the instructions that it finds in each cell. To be precise, the processor starts at cell number 0, it executes the instruction found in that cell and then moves on to cell number 1, then cell number 2, and so on. Of course, it could be that the processor encounters a cell that does not contain an instruction. In this case it might fail or simply ignore the cell and move on. However, there are also instructions which change the "flow of execution". These instructions are crucial, and we will get to them in a moment, but first we will describe the instructions needed for memory transfer and arithmetic.

The Instruction Set

We can divide the instructions that are understood by the processor into three groups:

• memory transfer,
• arithmetic, and
• flow control.

Very often, when instructions for a processor are described, three and four letter codes are used as the names of the instructions. We find this hard to understand, and instead we will write the instructions more or less like you might see in a high level programming language such as Python. However, in reality the instructions below are machine code, but that does not make them complicated. In fact, machine code instructions are typically much simpler than the instructions of a high level language, and here we have simplified things further, leaving out exotic instructions that are not essential to computation.

Memory Transfer

We need a way to refer to a specific cell in the memory of the SSMC. We will do so by writing memory[n] where n is the number of the cell that we wish to access. If you prefer to think of memory as a labelled box, n is the label.

With that in place, the following instruction tells the processor to transfer from long-term memory to short-term memory:

x = memory[n]

where, again, n is a number and x is the label of the cell in the processor's short-term memory. For instance, if n is 23, the instruction above tells the processor to move whatever is in cell 23 to x in the short-term memory. In place of n we could also have had one of the cells of the short-term memory, for instance i, and we could also transfer to another short-term cell. For example, y = memory[i] would also have been valid. The significant thing here is that the value of i is not known beforehand. Only when the program is actually running do we know what cell in memory, we move to y.

It is convenient to be able to assign a value directly to a short-term memory cell. In order to store 123 in the cell labelled x we simply write:

x = 123

Of course, this operation could also have been carried out by storing 123 in some memory cell, say 678, and then issuing the instruction x = memory[678].

We have seen how it is possible to transfer from long-term to short-term memory. We can also transfer the other way:

memory[n] = x

Before we describe other types of instructions, we will address three sources of potential confusion.

• For people familiar with a high-level programming language, memory[n], looks like we are accessing entry n in a list, and x seems to be a variable. The similarity is intentional, and we can, indeed, think of short-term memory as variables and long-term memory as a list of numbers. The instructions look similar to high level programming language statements, but here they are instructions to the processor. The transfer of memory is carried out directly by the hardware of our hypothetical computer.
• It was mentioned earlier that the instructions are also stored in memory as numbers. How does one store an instruction like memory[23] = x as numbers? While the details are complicated, the principle is simple. The instruction, memory[23] = x, can be described as "transfer contents of short-term memory cell x to long-term memory cell 23". Let us arbitrarily assume that the generic part of the instruction, i.e. "transfer contents of short-term memory cell to long-term memory cell", on its own is instruction number 17. That gives us an encoding of the instruction as a number, but we are still missing the two parameters 23 and x. Fortunately, 23 is clearly already a number, and we can assign a number to x; let us say that x is short-term memory cell 6. Now, we can encode the instruction with its parameters using just the three number 17, 23, 6. For a human being, memory[23] = x is much nicer to read than 17, 23, 6, but the processor would only understand the numerical encoding.
• The use of the equality symbol may be another source of confusion. Math teachers tell us that x = memory[23] means that x is the same as memory[23], and all of a sudden, we are saying that it means store the value of memory[23] in x?! We agree that this usage of = is confusing, and we could have used another symbol. However, in computer programs, a single equal sign is almost always used to indicate that the right hand side is stored in the memory location indicated by the left hand side. This is called assignment, and by introducing the use of = for assignment already now, we hope to avoid confusion later as you learn about programming.

Arithmetic

The SSMC can perform all of the four basic arithmetic instructions:

z = x + y
z = x - y
z = x * y
z = x / y

In the instructions above, the inputs, which we call operands, are always taken from x and y, and the output is stored in z. However, the SSMC is clever enough that you can use any cell in short-term memory as input or output for an arithmetic operation, for instance, z = a + i would be perfectly fine. You can also use numbers directly, and it is legal to assign back to the same short-term cell. For instance, to multiply a number by two, just write k = 2 * k.

There are no more mathematical instructions. This might seem surprising since there is a lot of mathematical functions that one might think we would need, but it turns out that with elementary school arithmetic, we can approximate the rest.

Flow Control

What is now needed are instructions that control the flow of execution. The following instruction changes the cell in memory where the processor reads its next instruction.

goto(m)

Normally, we would execute the instruction in cell n+1 after the instruction in cell n, but if cell number n contains the goto(m) instruction, the instruction in cell m is executed next.

Why would we want to jump like that? There are several reasons, but principally jumping to a different part of the program allows us to divide the program into smaller units, and we can often use a particular unit from several different places in a given program. This will be discussed in detail later.

We can also use goto as a simple way to stop execution. Consider what would happen if we put goto(n) into cell number n? Clearly, the next cell whose instruction should be executed would then be n but we are in n already so we simply repeatedly visit the same cell. This is not very elegant, though, so let us add a halt instruction:

halt

The next instruction is also a goto statement, but this time it is conditional.

if x < y: goto(m)

This instruction means that if x is less than y, then we transfer execution to cell m. Otherwise, we continue with the instruction in the next cell as usual.

As was the case for the arithmetic operations, we can use any of the short-term memory cells in the conditions of conditional goto statements, and we can also replace x or y with a specific number if needed. You may wonder if less than is the only type of comparison we need? The answer is yes since we can use less than to perform other tests too. For instance, we can test for equality using two less than comparisons: if x < y is not true and y < x is also not true, then x must be equal to y. For convenience, though, we might add more comparisons to an actual processor.

As noted, we only have the simple arithmetic instructions and not for instance square root, logarithm or other useful mathematical functions. These functions could have been added but are not essential. The SSMC instruction set is completely sufficient for performing any sort of computation, and we will prove that later in this text. In fact, we could do without some of the arithmetic operations. For instance, multiplication of two numbers could be substituted by repeated addition.

On the other hand, without the conditional goto the SSMC would not be a computer. It is hard to overstate the importance of conditional goto. Without this instruction the program would always follow the same flow of execution. With this instruction, we can let the data decide where the program goes next. It is a simple mechanism, but it turns out to be the essential ingredient of computing. Unlike the ordinary goto, the conditional variant can also be used to control loops. If we look back at the simple program in the introduction, we notice that lines 1 through 5 are repeated ten times. This is possible by the combination of using a short term memory cell, namely z, as a counter and a conditional goto. Each time the lines are exectuted, the program adds 1 to z, and when line 5 is reached the program jumps back to line 1, but only if z < 10. Thus, the conditional goto can be used to break out of loops when the condition fails - typically because we have looped for a predetermined number of times.

An SSMC Program

To illustrate what an SSMC program might look like, let us now consider a simple task.The operation we will consider is the sum of three pairs of numbers multiplied together. In the usual mathematical notation, we would write this operation in the following way,

$$\sum_{i=1}^{3} x_i \cdot y_i \enspace,$$

where each pair of numbers, $x_i$ and $y_i$, are multiplied and then added.

We can write x's and y's as two vectors $\mathbf x = [0.1, 0.8, 0.2]$ and $\mathbf y = [0.9, 0.1, 0.1]$. In this case, the answer is $0.9\cdot 01+0.1\cdot 0.8+0.1\cdot 0.2=0.19$, but how would SSMC arrive at that?

The following program performs the computation. The output is then written to cell number 20. The simulator has also been adapted to this program, and you can see it running here. The source for the SSMC simulator may also be of interest and is available here.

Program: Sum of Products

00: a = 0
01: i = 0
02: j = 14
03: k = 17
04: x = memory[j]
05: y = memory[k]
06: z = x * y
07: a = a + z
08: i = i + 1
09: j = j + 1
10: k = k + 1 
11: if i < 3: goto(4)
12: memory[20] = a 
13: halt
14: 0.1 
15: 0.8
16: 0.2
17: 0.9
18: 0.1
19: 0.1
20: 0

There are several things to note here. First of all, everything is in memory before the program starts. The instructions come first in lines 0 through 13, and the next six lines contain the input (the two lists of numbers), and finally cell 20 awaits the output. We are clearly seeing the contents of the memory before the program is executed since cell 20 contains 0!

Next, the program is surprisingly long. That is because the instructions that a processor understands are very simple. Each instruction does only a single thing whereas in a high level programming language, each line of code might result in quite a lot of computation. Moreover, we have to take care of every little thing. For instance, we cannot be sure what is in the short-term memory when the program starts, so we even have to explicitly assign 0 to a and i.

The following lines of Python code could have been used instead of the SSMC code above:

x = [0.1, 0.8, 0.2]
y = [0.9, 0.1, 0.1]
a = 0
for i in range(3):
    a += x[i] * y[i]

See how the last line fetches a pair of numbers from the two lists and multiplies them together and adds the result to a. This looks much simpler because each line does a lot more work, but under the hood, the Python code is transformed to something similar to SSMC code.

If you would like to try your hand at writing SSMC code, this Python script contains both the simulator and an example, and you can also provide an external file with the program. To try it out, download and then run it from the console using:

python ssmc_run.py

To get help, try

python ssmc_run.py -h

Exercises

This concludes the basic description of the SSMC. There are some exercises below aimed at testing your understanding of the principles.

1. List all the instructions that the SSMC processor understands.
2. Describe the two types of memory used by the SSMC.
3. Write a program that swaps two numbers in (long-term) memory using the same type of code as in the Sum of Products program.
4. Extend the program above such that the numbers are only swapped if the first number is greater than the second.
5. Extend the program above to sort a list of numbers.
6. Adapt the simulator to exercises 3-5.

2. Basic Computer Science

We can program the SSMC to solve any computational task, but based only on what we know so far, it would be very difficult to do in practice. We need some mechanisms for structuring computer programs, and we also need a way to make it possible to have several programs running at the same time. Finally, we need to somehow encode our data. In the following, we will try to explain how to achieve these goals. Along the way, we will also touch on some of the issues that are not pertinent to the SSMC but which we must consider in the context of real world computers.

Subroutines

While programs are written for computers, they will also be read by humans. This means that programs have to be comprehensible to people on top of actually doing what we intend them to do. Even well written programs are often hard to understand, and in poorly written programs finding bugs or making changes become impossibly hard tasks. This leads to the obvious question of what distinguishes good code from bad? There are many answers to this question, but readable computer programs tend to be broken up into small units that each have a clearly defined purpose. Fortuitously, there is an additional benefit to structuring a program in this way: if a program consists of discrete units - each with a clear purpose - we can often reuse the same unit in several places within the program, and we can even make libraries of such units that can be used from any number of programs. These units go by a variety of names; they are often called subroutines, functions, or procedures, or methods in object oriented programming. The oldest term seems to be "subroutine" and that is what we will use in the following.

When a subroutine is used from either the main program or from another subroutine, we say that it has been "called". After it is done, it "returns" to wherever it was called from. When we program in a high-level language such as C++ or Python, calling a subroutine is easy, and the underlying mechanism for making it happen is hidden from the programmer. However, we are here dealing with the SSMC. We do not get to enjoy the manifold luxuries of high-level programming.

At first glance, subroutine calling may not seem to require much drama. The SSMC processor understands the goto statement. It would appear that all we need to do is to have one goto which makes the program "jump" to the memory cell that contains the very first instruction of the subroutine. When the subroutine has completed, it should simply jump back to wherever it was called from by using another goto statement, or, to be more precise, it should jump back to the next cell after the cell whence it was called.

We seem to be doing fine, but did you notice the problem?

If we use a goto with a fixed address, we can only get back to one particular cell. This means that we can only call the subroutine from a single place which dramatically limits its usefulness. To be able to call the subroutine from several places, we need to, somehow, pass the return "address" to the subroutine.

There are many ways in which we could solve the problem. For instance, we can store the return address in short term memory. In our SSMC machine code, calling a subroutine, which we will assume starts in cell 1234, could now look like this

14: z = 16
15: goto(1234)
16: "program continues..."

When the subroutine has completed, it will goto(z) and this means that the first instruction after the return from the subroutine will be the one in cell 16.

At the outset, this will work, but it is a terrible solution. To understand why, consider what would happen in case a subroutine, which we will call A, calls another subroutine B. When A is called, the return address is stored in z, and later when A calls B we have to store the new return address (within A) in z. Now, imagine that B has been called and returns. The SSMC is executing instructions inside A, but now A hits the goto statement that should return the flow of execution to the main part of the program. To where does A return? Subroutine A returns to the memory cell to which B also just returned - simply because that is the address stored in z. It is very probable that the program is now stuck, forever executing the instructions between the cell to which B returned and the cell from which A would have returned to the main program except that the return address was to the aforementioned cell. Now, if there are just two subroutines, this may feel like a somewhat manageable problem. We could simply use different (short term) memory cells to store inputs and return addresses. However, consider what would happen if a subroutine were to call itself? This is called recursion and is fairly common, so it is not a hypothetical scenario, and in this scenario we still overwrite the short term memory cell containing the return address.

The Stack

Fortunately, a computer scientist named Edsger Dijkstra came up with a solution. The idea is to store the return address in a special place in memory called the stack [8]. Perhaps, the idea of the stack was inspired by the observation that when multiple subroutines are in play, they form a structure which is a bit similar to a physical stack of things. Observe that when we call a subroutine it does some work and then returns to the place from which it was called, regardless of whether that place is the main program or some other subroutine. Thus, if we have subroutine A calling subroutine B calling subroutine C, we can see them as forming a stack: C on top of B on top of A on top of the main program. This is much like a physical stack of flat objects.

The problem at hand is to retrieve the right return addresses wherever you are in this stack. Dijkstra's insight was that we can store the return addresses in a stack that perfectly matches the stack of subroutines. To make this scheme work, we need to set aside a part of the computer's memory for the stack and we need to store the address of the top of the stack somewhere, ideally in short term memory. When we store something on the stack, we simply put it on top of what was there before. This is called "pushing" and pushing involves adding one to the address of the top element and then storing the value we need to push at that location. Similarly, popping means that we subtract one from the address of the top element, effectively removing it from the stack.

The way function calling works is that we first push the return address onto our stack and then use goto to jump to the subroutine. When we need to return, we retrieve the address from the top of the stack, pop it, and again use goto to get back. Because we push when we call and pop when we return, the stack of return addresses matches the stack of subroutines perfectly, and it is always the right return address on the top of the stack.

This scheme is not only used for return addresses; it is one of the main ways that we use to set aside memory for computation. Whenever we need a memory cell to use for some computation, it is simply pushed onto the stack. Moreover, the data that a subroutine needs as input is also pushed onto the stack. The reader might worry that the stack will then start to diverge from the stack of called subroutines, but this is not the case because whenever a subroutine returns, it pops everything in reverse order of how it was pushed from within the subroutine: memory cells for computation inside the subroutine, input data, and, finally, the return address. Some subroutines might cause more to be put on the stack and others less, but when a subroutine has returned, all traces of it have been removed from the stack. Another concern could be that we now clearly need to access memory cells that are not on top of the stack, but that is not an issue. We do not need to know how tall the stack is. We simply need to know where the needed memory cell is relative to the top of the stack and then we can always access it. Since the data that is pushed onto the stack is always pushed in the same order when we call a subroutine, we always know where the data is relative to the top of the stack.

Understanding the stack is helpful for programmers. In particular, it is important to understand that the stack is a finite resource since a number of crashes of computer programs happen because the program runs out of memory set aside for the stack.

Understanding the stack is not only useful to prevent getting into trouble; understanding the stack can also help us find problems unrelated to the stack itself. In effect, the stack is a record of a sequence of subroutine calls. If your program crashes for whatever reason, that record can be stored (a bit like a fossil of a dead program) and used to quickly find out where something went wrong.

Side Effects and Return Values

Nothing prevents a subroutine from using a memory cell without pushing it onto the stack. In fact, this is necessary in some cases. Say we want the subroutine to record how many times it has been called. Clearly, this number must be stored somewhere other than the stack. If a subroutine does anything like this - anything that leaves a trace of it having been called, we say that it has side effects.

A subroutine without side effects is like a mathematical function which simply maps a value to a different value. As a trivial example, we could make a subroutine that squares a number. A subroutine for squaring would not need to have any side effects. It would, however, need to be able to transmit its output back to the caller. In fact, any subroutine without side effects and many subroutines that do have side effects also need some way of transmitting their output back to the caller. This can be done by passing the address of a memory cell where the output can be stored to the subroutine as part of its input. This is perhaps the best solution if the subroutine has a lot of output since we can pass the address of the first cell in a large contiguous chunk of cells. Another common solution is to store the so-called return value in a designated spot in short term memory. The caller is then responsible for moving it somewhere else if needed. For any subroutine that returns a single number that would be the most efficient solution.

Memory and Data

The presentation of memory has been a bit simplistic, and it is time to add a few details. Modern processors are so fast that it often takes much longer to get information from memory than to execute an instruction. Fetching from disk or network is, of course, much slower still. The software engineer Colin Scott has made a visualization of the time it takes to access various types of memory.

To mitigate the issues with slow memory access, real-world computers have yet another form of memory called cache. The cache is just a copy of cells in the memory that we have used recently, and this copy is kept on the processor itself. We are likely to use those cells again in the near future, and keeping copies very close to the processor is a really good idea. Of course, this means that the cache also has to record not just the contents of the cached cells but also their numbers. Fortunately, we do not have to store the number of each individual cell, since cells are actually stored in the cache in contiguous chunks called cache lines. This means that we only need to record where in the long-term memory the cache line is from and not each individual cell. It is also great because if we have just used one cell, we are likely to use the next. Thus, the cache lines tend to contain not just information we have used but also cells we will use in the near future. Below is an image illustrating how the cache is wedged between processor and memory.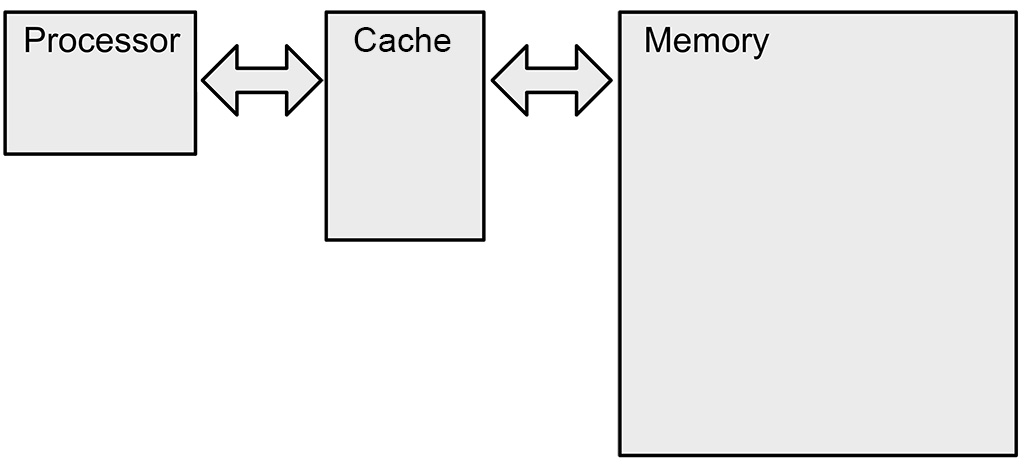

Note that physically the processor's cache is generally on the same chip as the processor itself. In fact, a large part of a modern CPU is cache.

Allocating Memory

Theoretically, we could allow programmers to use any cell in memory for data. Honestly, the way we have described the SSMC it is entirely up to the programmer to be disciplined about the usage of memory. Unfortunately, this is a recipe for disaster. It would be very easy for a program (by mistake) to write to a memory cell which contained an instruction. If this happens, the program will likely be corrupted, and the outcome is probably unexpected and hard to debug. The reason why it is hard to debug is that the program might reach the corrupted instruction a long time after the corruption occurred. In such cases, it can be very hard to figure out why the cell suddenly contains an illegal instruction.

To alleviate some of this issue, real computers set aside chunks of memory for each program, and these chunks are further divided into smaller chunks for the program code itself, the program's stack, and something called the heap which is where the program puts (often large) data that should not be tied to specific subroutines. Typically, the heap is allowed to grow and shrink while a program runs since the need for heap memory is hard to foresee ahead of time.

This division of memory into chunks is extremely helpful. Many program crashes are simply due to the program trying to use memory that is not set aside for it. While this is annoying it means that the program crashes when the program tries to write to the wrong memory cell. It does not happen later when some corrupted instruction is reached, and it is hard to overstate how much easier it is to find out why a program crashes if the crash and its cause are not separated in time! Of course, things are still not perfect. Many problems are still due to corruption of memory. For instance, we might need to store some data across several memory cells (set aside for data, e.g. on stack) but if we store numbers in four consecutive memory cells but in reality only set aside three memory cells then the last memory cell might have been set aside for something else, and once more we have problem that can be quite hard to debug.

It is fair to ask whether this is a real issue for casual programmers coding in, say, Python. It is clear that you are much better protected against memory issues if you program in Python (or a similar very high level language) than if you program in C. That said, memory issues can easily creep into most programming languages - particularly as we pursue efficiency gains.

Representing Data

The final thing that we should also briefly consider is about what sort of data that we can store in our computer's memory. The sad fact is that we can only store integers (meaning numbers such as 1, 2, 3, 4, ... ) in computer memory. This means that anything else has to be encoded as an integer. This also goes for instructions, and we have already discussed how an instruction can be encoded as a short list of numbers, and when we have many instructions, we simply string those numbers together in a much longer list. Unfortunately, this machine code is completely incomprehensible to human beings, but since the dawn of computers, engineers have assigned (usually three letter) alphabetical codes to each instruction. Replacing the numbers with these codes, we can turn machine code into assembly language which is also incomprehensible - except to assembly programmers. Hopefully, the SSMC code described in this text is just a bit less incomprehensible.

Moving on to other types of data than instructions, it is clear that we would often want to store text in a computer. If we want to store letters (characters) in computer memory, we also encode them by assigning a number to each letter. Maybe 'a' is 1, 'b' is 2 etc. Things get a bit harder when it comes to numbers with decimal places. How do we store a number such as 0.012 in a computer? the solution is simply to use exponential notation. Somewhat simplified, instead of 0.012, we store $12 \times 10^{-3}$. This is called floating point number representation because we raise 10 to some power (in this case -3) which determines where the point (or comma) is placed. This system works well, and if we know that this encoding is used, we only need to store the numbers 12 and -3. The downside is that floating point numbers cannot represent all possible real or even rational numbers. To make matters worse, floating point numbers become less and less precise the further they are from zero.

Multitasking

Most readers are probably aware of the fact that modern computers always have several programs running at once. Most of these programs do very mundane housekeeping tasks, and all of them are there to help improve your experience of using the computer (unless you have some malware).

Are these programs really running at the same time? On the SSMC this certainly would not be possible since it considers only one instruction at a time, but any modern laptop (or even smartphone) has multiple cores (at least two, but often 4-8 cores in fact). A core is an independent processor which shares some of the CPU resources with other cores on the same CPU, but a core is able to execute instructions independently of other cores on the same CPU (i.e. same chip). In other words, a meaningful difference between a real CPU and the SSMC processor is that in the former two (or more) programs can actually run in parallel. It is important, though, to be clear that while the SSMC can only perform a single task at a time that does not limit what it can compute. Moreover, by switching between programs, the SSMC can also make it seem as if it is actually executing several programs in parallel.

To understand how multitasking works on the SSMC, let us assume that we have two programs. The first program computes $n$ digits of $\sqrt{2}$ and the other program computes $n$ digits of $\pi$. We want these two programs to run as concurrently as possible. We can accomplish this by changing the programs such that they only do a limited amount of work and then yield the processor. For instance, the $\pi$ program might refine the current approximation of $\pi$ and store this approximation before yielding. To what does the program yield? It yields to another program which we call the scheduler. The scheduler alternately restarts the $\sqrt{2}$ program and the $\pi$ program. Each time they are restarted, they refine the approximations of their respective numbers until we reach the desired precision of $n$ digits. Then they inform the scheduler that they are done and the scheduler halts. At that point we will be able to retrieve all $n$ digits of $\sqrt{2}$ and $\pi$ from the SSMC.

It might seem that the $\sqrt{2}$ and the $\pi$ programs work a bit like subroutines, but there is a difference. Yielding is not returning. When a program yields, it does not pop the return address and the other memory it has used from the stack. Rather its stack is preserved, and the contents of its short term memory is stored in main memory. In this way it can take up the processing exactly where it left off. When the scheduler restarts a program, it restores the short term memory and then the program continues as if nothing had happened. Switching the short term memory and stack between processes is called a context switch and this is a core ingredient in multitasking. Since our simplistic processor cannot order a program to yield the processor, programs (which are to run concurrently) have to be written such that they yield the processor voluntarily, and this is a salient difference between the SSMC and a real computer. Any real computer's processor would be able to preempt a program. Preempting means that the processor preemptively stops the execution of one program, the scheduler takes over and switches to the context of the second program and lets that run for a while before switching back - or switching to yet another program, depending on the priorities of the programs. However, even on processors that are able to do preemptive multitasking, programs often yield the processor because they have nothing to do, e.g. because they are waiting for input: humans type very slowly, and a computer can do a lot of stuff while our fat fingers hover above the keyboard.

Finally, it should be noted that we usually talk about processes rather than programs when discussing parallelism and multitasking. It is better to talk about processes largely because it is entirely reasonable to run the same program twice in parallel with different inputs. For instance, we might want to write a program that computes $n$ digits of $\sqrt{x}$ for any number $x$ given as input. We might want to start two processes that both run the $\sqrt{x}$ program with $x=2$ and $x=3$ as their respective inputs in order to compute $n$ digits of $\sqrt{2}$ and $\sqrt{3}$ concurrently.

Exercises

1. We have heard about two mechanisms that could be used for doing the same thing repeatedly. The first is looping and the second is recursion. Consider the situation where we have a program that needs to run for a very long time. Is it better to use a loop or recursion and why? (Hint: stack)
2. If you have a lot of data, e.g. numbers, that needs to be processed, you can often structure computations such that if two numbers are processed consecutively they are also stored consecutively in memory. Explain why this is a good idea. (Hint: cache)
3. Explain the difference between preemption and yielding. Why could we do yielding but not preemption using the SSMC.
4. How would one store $\pi$ in a computer. Can we store $\pi$ as an exact real number or only approximately?

3. Computation

In the beginning of this text, we boldly claimed that understanding the SSMC is enough to understand any computer because anything computable can be computed by the SSMC. It is reasonable to wonder whether that is actually true. How do we know that if any computer can perform a given computation then so can our SSMC?

Before answering the question, we should make one thing clear: a computation may be infeasible due to lack of memory. Thus, the question is only whether all computers can run the same programs if they all have unlimited memory and unlimited time.

With this caveat, the answer is that computers can be used to emulate other computers, and that makes them equivalent: given two computers A and B, we can write software for B such that it behaves exactly like A and executes any program that A could execute. Of course, if A is a very powerful computer and B is not, then the task of emulating A and then running a specific program might cause B to spend millenia on a computation that would run in seconds on A. That does not matter for the central argument.

However, showing that the SSMC can emulate a specific computer might be tedious. It seems that we need some model computer that is even simpler than the SSMC and for which we can prove that emulation is possible with only moderate effort. In his work on proving the limits of what is computable, Alan Turing famously came up with a solution to this problem by inventing the so called Turing machines. A Turing machine is a purely theoretical device which manipulates symbols stored on an infinitely long tape, and we can design Turing machines for various tasks. For instance, we could make a Turing machine for adding, subtracting, multiplying, or performing any other arithmetic operation on numbers encoded on the tape. We could also make a Turing machine that writes out all the numbers belonging to some sequence on the tape, e.g. all the primes, digits of pi, or the $\sqrt{2}$. In fact, it is generally believed that anything which can be computed can be formulated in such a way that it can be computed by some Turing machine. There is no proof of this, but nobody has come up with a computation which can be performed by some specific non-Turing machine but not by any Turing machine. Thus, we regard the space of computations which can be performed at all as the space of computation which can be performed by Turing machines.

Now, one specific type of Turing machine is especially important: a Universal Turing Machine (UTM) is a Turing machine which is general enough that it is possible to encode the instructions for any other Turing machine on the tape. This means that we only need a universal Turing machine to perform a computation that can be performed by any Turing machine. By extension, in order to prove that any system for computation, i.e. a physical machine together with a method for programming it, can emulate any Turing machine, we just need to show that it can emulate a UTM. Formally, we say that a system for computation is Turing complete, if it can be used to emulate a universal Turing machine either directly or through a chain of emulations. In other words, we don't have to show that the SSMC can emulate a real computer, we only have to show that it is Turing complete. To do so, we "only" have to show that the SSMC can emulate some system - any system - which is itself known to be Turing complete.

Rule 110

To show that the SSMC is Turing complete, we could show that it is possible to emulate a universal Turing machine using our SSMC. However, it is possible to do something even simpler. As just discussed, we only need to show that we can emulate something that can itself emulate a UTM. Hence, we will pursue a less demanding strategy and instead look for the simplest Turing complete system we can find. One of the simplest such systems is a so called one dimensional cellular automaton that was introduced by Steven Wolfram. It is called Rule 110 and was proven to be Turing complete by Cook [2]. Emulating Rule 110 will be our goal in the following.

To understand Rule 110, we need to first understand how 1D cellular automata work. We will start by assuming that we have a list of digits which are all either 0 or 1. The list could look like this:

0 1 0 0 0 1 0 1 0 1 1 1

A cellular automaton can be understood as a machine - in the same abstract sense as Turing machines - that is associated with one of these digits. There are 12 digits, hence we have 12 automata, and we can think of the value of each digit as the "state" of the associated automaton (or machine). Now, every automaton can do precisely one thing: it can change its state from 0 to 1 or vice versa. At the outset this seems to be a very limited scheme, but it becomes much more interesting when we add the simple mechanism that an automaton should take the values of its neighbors into account.

For instance, we might make the rule that an automaton should change its state to 0 except in the case where its own state is 1 and both its neighbors are also 1. In this case it keeps on being in state 1. If we apply this simple rule, we get a new list of digits

0 0 0 0 0 0 0 0 0 0 1 0

Of course, there is a slight wrinkle. How do we deal with the leftmost and the rightmost digits since they lack a neighbor? One way of handling this conundrum is to assume that the missing neighbors are always 0 which is what I did above. Another important detail is that we do not update the list as we go along. If we immediately updated the digits then the new state of an automaton would influence the state changes of automata which are updated later. Instead, we produce a new list of digits and then replace the old list with the new when we are done.

With this in place, we can move on to Rule 110 which is a bit more advanced. Instead of the verbal explanation above, we will describe the rule by showing all possible configurations of a digit and its left and right neighbors. Below, we show what happens to the middle digit which is the one associated with the current automaton. Since there are eight possible different triples of binary digits, we only need eight rules, and the full set of possible state changes in Rule 110 are as follows:

1 1 1   1 1 0   1 0 1   1 0 0   0 1 1   0 1 0   0 0 1   0 0 0
  0       1       1       0       1       1       1       0

Presented like this, we are also in a position to understand why it is called Rule 110. The digits that result from applying the rule, i.e. the lower digits, form the binary number 01101110 which is 64+32+8+4+2=110 in decimal.

If we apply Rule 110 to the original string, we get:

1 1 0 0 1 1 1 1 1 1 0 1

For visualization purposes, there is a better way of showing the workings of the cellular automata than as a simple list of digits. Using a scheme that was introduced by Steven Wolfram, we can show the automata after the rule has been applied below the automata from before the rule was applied. If we draw 1 as a black pixel and 0 as a white pixel, we get an interesting pattern where the vertical axis is time, and it suddenly becomes very clear how the automaton changes over time.

The image below shows Rule 110 applied for ten iterations using this type of visualization. In the initial list of digits at time 0 only a single automaton had state 1.

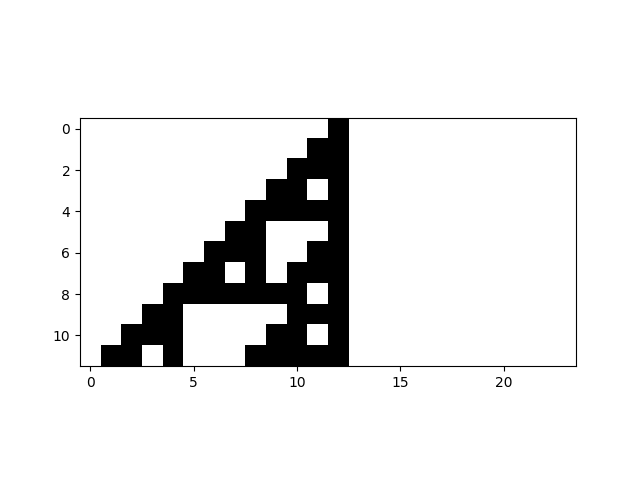
Honestly, it is not clear how to do computations using Rule 110. If we wanted to perform some computation such as, say, adding two numbers, it would be possible to prepare the list of digits in such a way that the numbers and the operation are encoded, and simply by running Rule 110 we would finally arrive at the result (encoded somehow). But, I have no idea how to do this in practice, and I am not sure anybody ever tried. However, it was conjectured by Wolfram and proven by Cook [7] that Rule 110 is Turing complete which means that it must be possible in theory - even if it is not really practical.

Fortunately, we don't have to do any computation using Rule 110. We just have to show that we can write a program that emulates Rule 110 and run it on the SSMC. That is much less difficult, and a program written in SSMC machine code that runs Rule 110, thereby proving the Turing completeness of the SSMC, is shown below:

00: k = 0
01: i = 0
02: i = i + 1
03: j = i + k
04: x = j + 37
05: y = j + 38
06: z = j + 39
07: a = memory[x]
08: b = memory[y]
09: c = memory[z]
10: y = y + 24
11: if a == 0: goto(23)
12: if b == 0: goto(18)
13: if c == 0: goto(16)
14: memory[y] = 0
15: goto(34)
16: memory[y] = 1
17: goto(34)
18: if c == 0: goto(21)
19: memory[y] = 1
20: goto(34)
21: memory[y] = 0
22: goto(34)
23: if b == 0: goto(29)
24: if c == 0: goto(27)
25: memory[y] = 1
26: goto(34)
27: memory[y] = 1
28: goto(34)
29: if c == 0: goto(32)
30: memory[y] = 1
31: goto(34)
32: memory[y] = 0
33: goto(34)
34: if i < 23: goto(2)
35: k = k + 24
36: if k < 264: goto(1)
37: halt

The program may be a bit hard to read, and it might behove us to explain precisely what it does. Basically, it puts itself in the position of each automaton in turn and looks up its current state and the state of its neighbors (lines 7, 8, 9), storing these in short term memory locations a, b, and c. Then it applies Rule 110 (lines 11 through 33) which includes writing the new state of the automaton to a different memory location. Thus, this program also keeps the old state of every automaton. The remaining lines ensure that all automata are visited and that the update of all automata happens a total of 10 times. If you would like to see the SSMC running Rule 110, here it is. In the linked to webpage, you also see the working memory and how it changes as the program runs. In the initial list of digits, only one digit is 1.

Admittedly, the program was tedious to write due to the many numbers that were needed to indicate memory locations for states and instructions, and there were several bugs along the way. SSMC machine code is not as convenient as a high level programming language. On the other hand, it is far easier to code for the SSMC than for Rule 110. Arguably, that is ironical since the simplicity of Rule 110 makes it easy to use for a proof of Turing completeness.

Now that we know the SSMC is Turing complete, we can celebrate by considering what the secret ingredient for Turing completeness might be. Looking at the code it quickly becomes clear that apart from the basic arithmetic it contains many goto statements and also conditional goto statements. Without the conditional goto statements, or something equivalent, we could not have achieved Turing completeness. This is clear since the program needs to make different decisions based on the values of the three digits under consideration, and the conditional goto statements are effectively our tool for making decisions.

At a slightly higher level of abstraction, giving the computer a way to decide what to do next is key to general computation. It is very analogous to the difference between a joy ride in an amusement park and a rail system where you can change tracks. The joy ride is always the same whereas a rail switch which allows you to change tracks can take you wherever you have laid down tracks.

The Decision Problem and the Halting Problem

When Alan Turing invented the Turing machines discussed above, the larger goal was to answer a question that had been posed earlier by the German mathematician David Hilbert. Hilbert's question is called the decision problem, or the "Entscheidungsproblem" in German, and what is at issue is whether all mathematical statements can be proved or disproved "mechanically" [2]. To be more precise, Hilbert (before any computers existed) wanted to know if it would be possible to come up with a stepwise procedure that would take a statement as input and produce the answer true if the statement were true and false otherwise.

Penrose gives several examples of what such a statement might be [4]. One of these examples is the conjecture by Goldbach that every even integer greater than two can be written as the sum of two primes. This has not yet been proven, but it is trivial to write a program that finds prime numbers, at least if efficiency is not a concern. Consequently, for any even number we can check whether that number is the sum of a pair of primes, and it would not be hard to write a program, $G$, that enumerates all even numbers and checks whether each is the sum of two primes. $G$ would run for ever, except if it were to encounter an even number that is not the sum of any pair of primes. In this case, we have found a counter example. The Goldbach conjecture would be false, and the program should halt.

This reasoning leads to an interesting approach for testing whether the Goldbach conjecture is true or false: if we can make a computer program that tells us whether another program ever halts - or if it goes on forever (or until you pull the plug) - then we are done. Let us assume we have such a program and call it, $H$, short for the halting program. The input to $H$ is some other computer program, for instance the Goldbach program $G$, and the output is true if $G$ stops and false otherwise. With $H$ we no longer have to wait forever to find out if the Goldbach conjecture is true since $H$ (which we assume exists) will stop after a finite amount of time, and its output will inform us about whether $G$ would stop if we ran it. If $G$ would stop, the Goldbach conjecture is false. If $G$ would run forever, it is true.

In fact, $H$ could be used not just for the Goldbach conjecture but as a means of proving any formal statement. This assumes, of course, that $H$ is general and also works on other programs than $G$. In the following, a very informal argument for why this is true will be given, largely following Penrose's book.

Given some formal symbolic language for mathematical statements, we can use a computer program to systematically write out a long list of all possible statements expressible in said formal language. Some of the statements will be proofs of other statements. Now, if a statement actually has a formal proof, the proof is going to be somewhere in the list since it contains all possible statements. Thus, if there is a proof of a given statement, the program will eventually reach it and (you guessed it) halt.

One might think this statement listing program would - in itself - be enough to solve the decision problem. It seems that all we have to do is wait. Given any statement, the statement listing program will arrive at either its proof or the proof that it is false. The program will probably not be fast, but it should work.

Unfortunately, this scheme does not work. As Alan Turing observed [9], Kurt Gödel's incompleteness theorem gets in the way: given any formal system for expressing mathematical statements, there are statements which we cannot prove using the system, nor can we prove that they are false. Thus, for some mathematical statements we would wait forever before their proofs are listed, but there is no point in time when we can say with certainty that the program will never stop. There is simply no way of knowing whether the proof listing program will eventually get to our proof if we wait a while longer.

However, everything changes if we have our assumed halting program, $H$. If a given statement is true, the proof will be in the list, and $H$ must report that the program would terminate if run. Conversely, if the proof is not in the list, $H$ returns false. Of course, the proof might be missing for two different reasons. It could be missing because the statement is false and there is a proof to that effect, and it could also be missing because there is a proof of neither the statement nor its negation. To distinguish between these two cases, we can simply run $H$ again to check if the negation is in the list. Thus, we can, in fact, use the halting program to tell us definitively whether a statement is true or false or undecidable within our formal system.

The upshot is that a lot is riding on the existence of $H$. If it exists, we have a solution for the halting problem and hence the decision problem. So does it work? Is there some completely general algorithm for analyzing programs that can tell us with certainty whether any program halts? To figure this out, let us assume the answer is "yes" and design a new program. This program, which we will just call $P$, receives as its input another program $Q$. The halting program $H$ is a part of $P$, and we use $H$ to check whether $Q$ runs forever or stops. If $H$ reports that $Q$ would run forever, then $P$ stops. Otherwise, $P$ runs forever - because we deliberately add a goto statement that makes it go back to the same line, until someone cuts the power to our imaginary computer.

Nobody claims that $P$ performs any useful computation, but it would definitely work as intended for almost any input program $Q$. However, what if someone assigned $Q=P$? In other words, what would happen if we ran $P$ using $P$ itself as the program to run the halting program on. I know this might feel very contrived, but nothing would prevent us from encoding $P$ as data and then passing $P$ to itself as input. On the other hand, it does lead to a contradiction. If $H$ determines that $P$ runs forever, then $P$ stops, and if $H$ determines that $P$ stops, well, then it runs forever. That it feels contrived does not matter: $P$ does exactly the opposite of what $H$ determines that $P$ will do. This is a paradox which entails that we have made a wrong assumption. The only assumption we have made is that $H$ exists. Consequently, this must be false, and $H$ does not exist. This means that there is no general solution to the halting problem and therefore no general solution to the Entscheidungsproblem.

4. Computers in the Real World

The SSMC does not exist, but if we made a few things a bit more precise, it could exist, although it would feel like a very old machine (like a computer from the fifties) due to its lack of input output devices. Throughout the last half of the 20th century, computers gained storage devices, keyboards, screens, multiple CPUs, peripherals such as printers, network interfaces, and ultimately auxiliary highly parallel processors in the form of graphics cards. In other words, computers became systems in which the central processor(s) was (or were) just a single component. Any number of devices connected to the processor(s) would take care of a range of tasks, usually pertaining to input/output and external storage of data. This is why we got operating systems. Even a seemingly mundane task such as reading from a hard disk would be very tedious if the programmer had to specify all details about how to find the file and retrieve the bits from the physical device. Operating systems helped insulate us from the physical hardware of the devices.

While arriving at the vast complexity of a modern computer required incredible feats of engineering, the journey from something as simple as the SSMC to the modern computer has been swift whereas it has taken us a long time to get to the level of the SSMC. Arguably, this is surprising. Not least because machines that help people compute by performing basic arithmetic have been around for a long time. Making a machine that can perform basic arithmetic is difficult, but it does not require modern technology. The two great mathematicians Pascal and later Leibniz both made their own mechanical calculators, and there are many other examples, notably Charles Babbage's somewhat ill fated Difference Engine. More recently, the small Curta calculator was popular up until the middle of the 20th century. It is also not the case that you have to use either mechanics or electronics for performing computation. Say you have two vials of fluid. Simply pouring the contents of both into a measurement beaker will give you the sum of the fluid volumes contained in the vials. Thus, using fluid we can perform addition very easily. This may sound silly, but in the early 20th century Russian scientists developed a machine for integration based on fluid which was apparently in active use until the eighties.

However, allowing the machine to change tracks is something else. Before the 20th century, it seems that only Charles Babbage had even conceived of a machine that would be able to do that, but his Analytical Engine was never realized. Probably, the conditional goto (track changing) is difficult to do with a mechanical system. In principle, almost any type of physical process could be harnessed for computation, but unlike simple arithmetic or integration, making a machine that decides what to do seems to require a complex machinery which is much easier to do with electronics.

The electrical relay provided a path via electronics (or electromechanical systems anyways), and in 1941 the german engineer Konrad Zuse created the Z3 which was the first true electronic computer. Actually, it did not have conditional goto but it was in theory possible to work around that. The successor, Z4, became the first commercially sold computer when it was delivered to the ETH in Zürich. To get a deeper understanding of how we can build a computer from simple electronics, Charles Petzold's book [1] is warmly recommended.

Konrad Zuse worked in Germany, but electronic computers were also being developed in the USA during the Second World War. A good example is the Mark 1 computer designed by Howard Aiken and built by IBM. The Mark1 was electromechanical like Zuse's machine. Grace Hopper was one of the programmers of the Mark 1, and she went on to make important contributions to computer science. In particular, she invented the idea of a compiler which is a computer program that transforms a readable high level computer program into machine code. Beyer's book [3] presents a very readable account of Hopper's life and work.

Just like the German machine, the American computers were used to aid the war effort. The Hungarian mathematician, and by all accounts genius, John von Neumann had been one of the early users of the Mark 1 as well as other early computers, and in 1945 he synthesized his understanding of the principles in the "First Draft of a Report on the EDVAC." Most "first draft reports" are not published, but when von Neumann's collaborator Herman Goldstine received the report he sent it to everyone who might be interested, and thus the principles of a modern computer became available to all who cared. These principles also became impossible to patent which made some people very unhappy. The unusual life of John von Neumann and his many contributions to science and math are discussed in Bhattacharya's book [2]. Like almost any other computer, the SSMC is designed according to the von Neumann architecture.

References

1. Petzold, Charles. "Code: The hidden language of computer hardware and software." Microsoft Press, 2000.

2. Bhattacharya, Ananyo. "The Man from the Future: The Visionary Life of John von Neumann." Allen Lane, 2021.

3. Beyer, Kurt. "W. Grace Hopper and the invention of the information age." MIT Press, 2012.

4. Penrose, Roger. "The emperor's new mind: Concerning Computers, Minds and The Laws of Physics." Oxford University Press, 1989.

5. Penrose, Roger. "The road to reality." Random house, 2006.

6. Gertner, J. "The idea factory: Bell Labs and the great age of American innovation". Penguin, 2012.

7. Cook, Matthew. "Universality in Elementary Cellular." Complex Systems, 15(1), 2004.

8. Dijkstra, Edsger Wybe. "Recursive Programming." Numerische Mathematik 2.1 (1960): 312-318.

9. Turing, Alan Mathison. "On computable numbers, with an application to the Entscheidungsproblem." Journal of Math 58.345-363 (1936): 5.