Neural Representation of Open Surfaces
Thor Vestergaard Christiansen, J. Andreas Bærentzen, Rasmus R. Paulsen and Morten Rieger Hannemose
Paper at The Symposium on Geometry Processing (SGP) 2023
Example of interpolations between shapes with different number of boundary curves (a pair of pants and a shirt)
Abstract
Neural implicit surfaces have emerged as an effective, learnable representation for shapes of arbitrary topology. However, representing open surfaces remains a challenge. Different methods, such as unsigned distance fields (UDF), have been proposed to tackle this issue, but a general solution remains elusive. The generalized winding number (GWN), which is often used to distinguish interior points from exterior points of 3D shapes, is arguably the most promising approach. The GWN changes smoothly in regions where there is a hole in the surface, but it is discontinuous at points on the surface. Effectively, this means that it can be used in lieu of an implicit surface representation while providing information about holes, but, unfortunately, it does not provide information about the distance to the surface necessary for e.g. ray tracing, and special care must be taken when implementing surface reconstruction. Therefore, we introduce the semi-signed distance field (SSDF) representation which comprises both the GWN and the surface distance. We compare the GWN and SSDF representations for the applications of surface reconstruction, interpolation, reconstruction from partial data, and latent vector analysis using two very different data sets. We find that both the GWN and SSDF are well suited for neural representation of open surfaces.
Results
Interpolations between shapes with different boundary curves
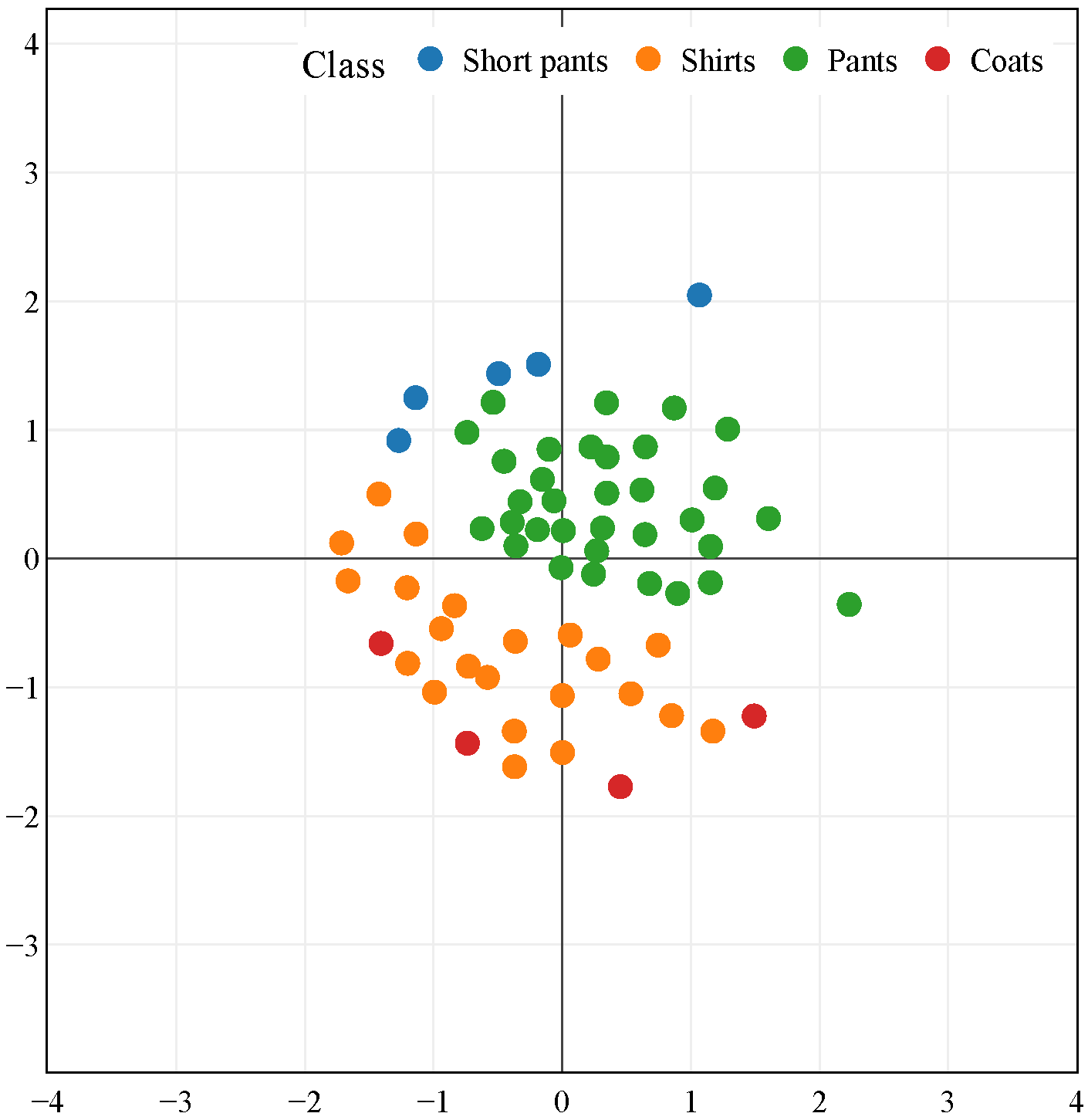
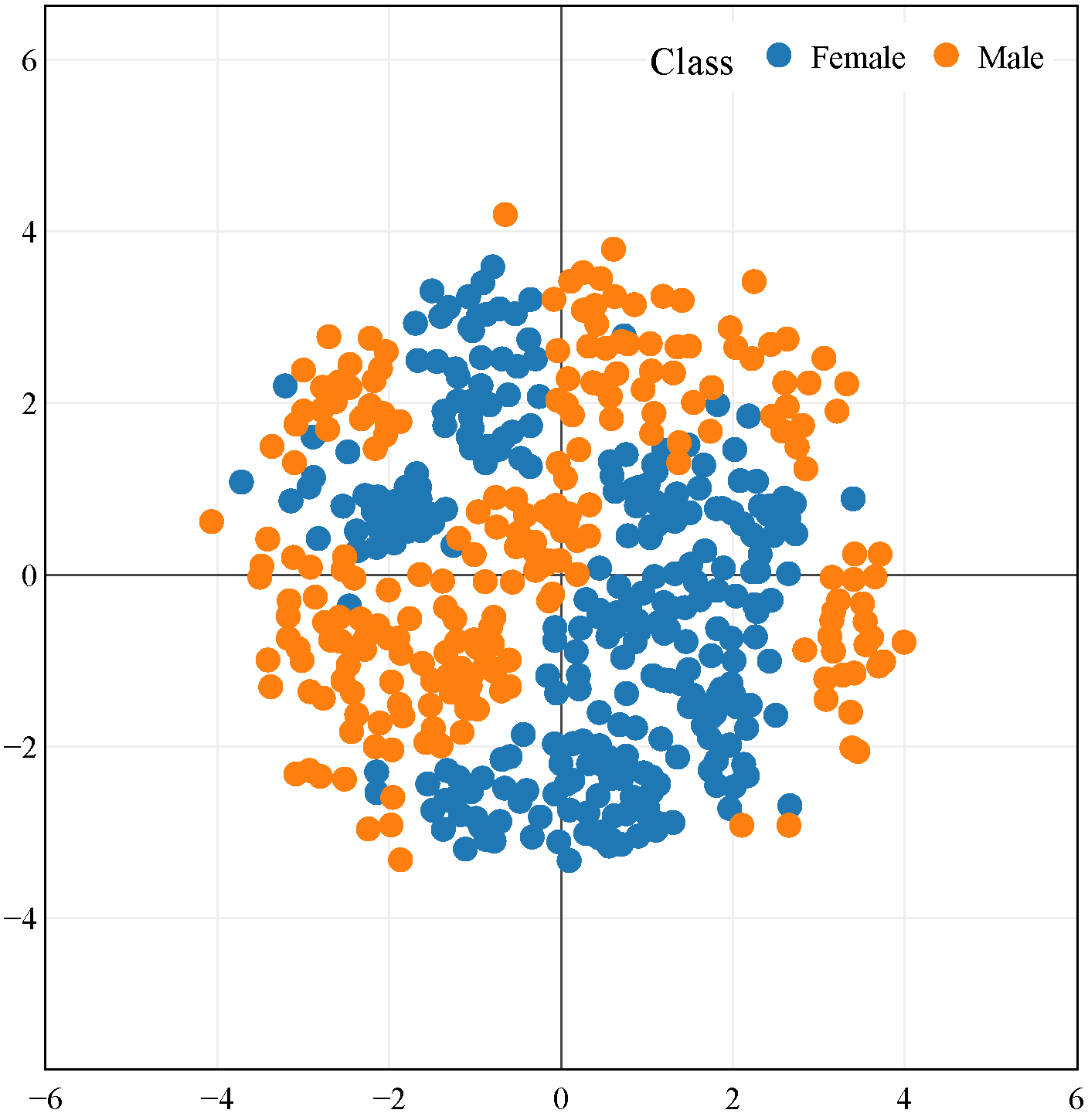
Clustering of shapes with similiar topology and geometry in latent space using Multidimensional Scaling for visualization in 2D
Future work / Research Directions
- Constraining the latent vectors during shape completion using e.g. L2-regularization to obtain better shape completions.
- Incorporating the Semi-Signed Distance Field for geometry representation in NeRF.
- Using Semi-Signed Distance Fields to represent open surfaces in diffusion models inspired by HyperDiffusion: Generating Implicit Neural Fields with Weight-Space Diffusion - Perhaps using it to create different types of garments?
- Using Semi-Signed Distance Fields to represent 3D scenes - inteporlate between different scenes, cluster scenes according to room-type and do partial shape completion.
- Use Semi-Signed Distance Fields to represent different types of tissue for classification tasks similar to Implicit Neural Distance Representation for Unsupervised and Supervised Classification of Complex Anatomies.
Data sets
In this paper we used the BU-3DFE and the MGN data set. Finding data sets with open surfaces is difficult, which is why we used the the BU-3DFE and MGN data sets. However, we have later been notified about the following data sets: Garments and 3D Scenes.
If you find our work useful, please cite the paper:
BibTeX:
@article{christiansen2023a,
author = {Christiansen, T. V. and Bærentzen, J. A. and Paulsen, R. R. and Hannemose, M. R.},
title = {Neural Representation of Open Surfaces},
language = {eng},
format = {article},
journal = {Computer Graphics Forum},
volume = {42},
number = {5},
pages = {e14916},
year = {2023},
issn = {14678659, 01677055},
publisher = {John Wiley and Sons Inc},
doi = {10.1111/cgf.14916}
}
This template is kindly borrowed from Christian Keilstrup Ingwersen.
Page updated on the 15th of July 2023.