Appendix A

Implementation of Blocks Common to Most Radices

Introduction

The functional blocks described in this appendix are those blocks common to most of the implementations presented in this work.

A.1 Register

All the registers are implemented by using arrays of flip-flops. The flip-flops are D-type edge-triggered on the rising edge and include either SET pin, or RESET pin, or both.

A.2 Carry-Save Adder

The radix-2 carry-save adder is implemented as an array of full-adders. Each full-adder (FA) is implemented as depicted in Figure A.1 and it can be decomposed into two half-adders (HA). Its maximum delay is the delay of the two XOR gates, or half-adders (t_FA = t_HA + t_HA).

Figure 1.1: Implementation of full-adder.

A.3 Selection Function

The selection function (SEL), except for radix-512, is usually composed by a small carry-propagate adder, because of the carry-save representation of the residual, and by a function implemented with logic gates as depicted in Figure A.2. The implementations of SEL are obtained by synthesis of the VHDL description of the selection function. SEL includes both the assimilation of the carry-save representation of [^y] and the actual digit-selection function.

Figure 1.2: Selection function.

A.4 Multiple Generator

The multiple generator (MULT) perform the following operation for division:

-q_j+1 d .

In order to avoid the implementation of a complicated multiple generator, the quotient digit is represented in a 1-out-of-h code. In this work, most of the result-digits are represented as signed-digit numbers with values in the set {-2,-1,0,1,2}. Four signals (h = 4) are used to represent these five values with the code given in Table A.1. This representation makes the multiple generator simple, as shown in Figure A.3.

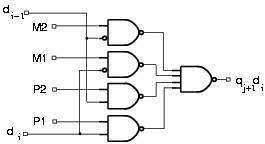
Figure 1.3: One bit of the multiple generator.

digit	M2	M1	P1	P2
-2	1	0	0	0
-1	0	1	0	0
0	0	0	0	0
1	0	0	1	0
2	0	0	0	1

Table A.1: Result digit encoding.

A.5 Sign-and-Zero Detection Unit (SZD)

To perform the rounding, it is necessary to detect the sign of the residual from its redundant representation and to determine if the residual is zero. In [10], a network to detect the two conditions: sign of residual, and residual is zero, is described. We now summarize its implementation. Let w_S and w_c be the values of the (h+1)-bit carry-save representation of the last residual. We introduce two quantities a_S and a_C such that

a_S + a_C = w_S + w_C - 2^-h

and consequently, the condition w_S + w_C = 0 results in

a_S + a_C = 2^-h

Therefore, the final residual is zero when:

zero =

h
Õ
i = 0

P_i =

h
Õ
i = 0

a_Si Åa_Ci

(25)

where a_Si and a_Ci, which assume either value 1 or 0, represent the bits in position i in the carry-save representation. The sign can also be detected by using a_Si and a_Ci by observing that:

a_S + a_C ³ 0 Þ w_S + w_C > 0

and

a_S + a_C < 0 Þ w_S + w_C £ 0

Therefore:

sign = ( a_S0 Åa_C0 Åc_MSB )

zero

where c_MSB is the carry into the most-significant bit.

The subtraction of 2^-h to the carry-save representation of w is done by adding a (h+1)-bit vector of 1s. The resulting expression for the bits of a_S and a_c are

a_Si =

(w_Si Åw_Ci)

and a_Ci+1 = w_Si + w_Ci

(26)

The P_is of expression (A.2) are generated in a hierarchical way using a carry-look-ahead structure. For example, for a 64-bit sign-and-zero detection unit using groups of 4 bits we have the scheme of Table A.2. And the two corresponding expressions for zero and sign are:

zero = P

and

sign = ( G Åp₆₃ )

Level 0

g_i = a_Si a_Ci and p_i = a_Si + a_Ci

i = 0, 1, ¼, 63

\hline

Level 1

for each j = ë[i/4] û and corresponding g_k, p_k with

k = i mod 4

G_j = g₃ + g₂ p₃ + g₁ p₂ p₃ + g₀ p₁ p₂ p₃

j = 0, 1, ¼, 15

P_j = p₀ p₁ p₂ p₃

\hline

Level 2

for each l = ë[j/4] û and corresponding G_k, P_k with

k = j mod 4

G^*_l = G₃ + G₂ P₃ + G₁ P₂ P₃ + G₀ P₁ P₂ P₃

l = 0, 1, 2, 3

P^*_l = P₀ P₁ P₂ P₃

\hline

Level 3

G = G^*₃ + G^*₂ P^*₃ + G^*₁ P^*₂ P^*₃ + G^*₀ P^*₁ P^*₂ P^*₃

P = P^*₀ P^*₁ P^*₂ P^*₃

Table A.2: Carry-look-ahead tree for 64-bit SZD.

A.6 Voltage Level Shifter

In this section we describe the voltage level shifter presented in [35]. Voltage level shifters are needed in circuits that operate with dual voltage (V_DD regular supply voltage and V₂ reduced supply voltage). Level shifters are necessary when a portion of the circuit at voltage V₂ is connected to a portion at voltage V_DD. As shown in Figure A.4, if the output of a circuit operating at V₂ (C2) is connected directly to the input of a circuit operating at V_DD (C1), static current flows in C1 at the input level "high". Since the voltage of node N1 is not raised higher than V₂, the p-transistor MP1 cannot be cut-off if V₂ < V_DD - V_threshold,p . Therefore, static current flows from V_DD to V_SS through MP1 and MN1. In order to block this static current a voltage level shifter is inserted at node N1. No level shifting is necessary when, in the reversed case, the output of a V_DD operated circuit is connected to the input of a V₂ circuit. The voltage level shifter is realized as depicted in Figure A.5. Table A.3 indicates the input-output delays and energy consumption for a level shifter operating at V_DD = 3.3 V and V₂ = 2.0 V, and its comparison with an inverter of the Passport library. The values in Table A.3 were obtained by SPICE simulation.

Figure 1.4: Dual voltage: C1 is not cut-off.

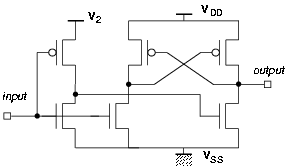
Figure 1.5: Voltage level shifter.

	level shifter					inverter
	delay [ns]				E_tran	delay [ns]				E_tran
	t_LH	t_rise	t_HL	t_fall	[nJ]	t_LH	t_rise	t_HL	t_fall	[nJ]
SL1	0.144	0.13	0.042	0.11	0.7	0.097	0.20	0.094	0.16	0.3
SL4	0.245	0.17	0.087	0.22	1.2	0.164	0.32	0.163	0.27	0.8
SL16	0.670	0.45	0.271	0.69	3.4	0.459	0.98	0.476	0.86	2.1

SL = standard load = 22 fF for Passport library

Table A.3: Delay and energy comparison between level shifter and inverter.

File translated from T_EX by T_TH, version 1.1 and by M_E. Last Modified : Fri Jul 9 11:14:40 PDT 1999