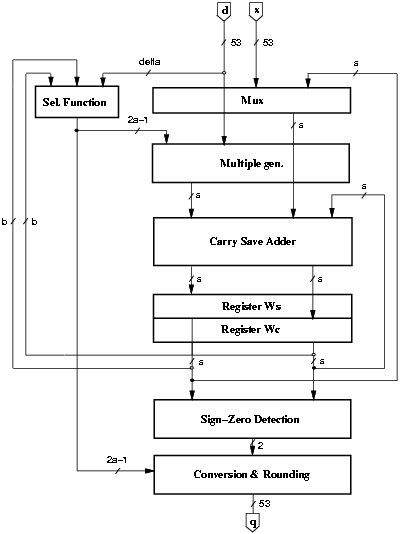
Figure 2.1: Block diagram of radix-r division.
In this chapter the division and square root algorithm are summarized. In the first part of the chapter, we describe the digit-recurrence algorithm for division, the on-the-fly conversion and rounding algorithm and give an example of division performed with the two algorithms. Then two modifications to the division algorithm are discussed to make it suitable for high radices. Finally, the square root algorithm and its combination with division are described.
Digit-recurrence algorithms for division and square-root give probably the best tradeoff delay-area [29], and are the focus of this work. Digit-recurrence algorithms produce a fixed number of result bits every iteration, determined by the radix. Higher radices reduce the number of iterations to complete the operation, but increase the cycle time and the complexity of the circuit.
The division algorithm, described in detail in [10], is implemented by the residual recurrence
| (7) |
| (8) |
The quotient digit is in signed-digit representation {-a, ¼,-1,0,1, ¼, a} and the residual w[j] is stored in carry-save representation (wS and wC). The quotient digit is determined, at each iteration, by a selection function
|
|
| (9) |
The signed-digit representation of the quotient must be converted to the conventional representation in 2's complement; the on-the-fly convert-and-round algorithm performs this conversion as the digits are produced and does not require a carry-propagate adder.

Figure 2.1: Block diagram of radix-r division.
A possible scheme to perform the division algorithm is shown in Figure 2.1. The recurrence is implemented with the selection function (SEL), the multiple generator (MULT), the carry-save adder (CSA) and two registers (REG) to store the carry-save representation of the residual. The number of bits in the recurrence (s), depends on the radix r and on the redundancy factor r = [a/(r-1)]. Because of the carry-save representation of the residual, the selection function in Figure 2.1 is composed by a b-bit carry-propagate adder and a logic function.
The conversion block performs the conversion from the signed-digit quotient and the rounding according to the sign of the final residual and the signal that detects if it is a zero, which are produced by the sign-zero-detection block (SZD). The scheme is completed by a controller (not depicted in the figure).
This algorithm is used effectively for radix 2, 4 and 8. For higher radices the selection function is too complex and its delay too high.
We summarize the on-the-fly convert-and-round algorithm described in full detail in [10]. Three registers are needed to store Q, QM, and QP (Figure 2.2). However, as explained later, when the rounding is done in the least-significant position, and a < r-1 two registers Q and QM are sufficient.

Figure 2.2: Convert and round unit.
The rounding is done using the round-to-nearest-even scheme, which is mandatory in the IEEE standard [28]. The other rounding schemes are not discussed here, but they can be realized with the same unit used for the round-to-nearest-even case.
After iteration j the three registers contain
|
|
Q[j] Ü ( shl( Q[j-1] ), qj ) if qj > 0
QM[j] Ü ( shl( Q[j-1] ), qj - 1 )
Q[j] Ü ( shl( Q[j-1] ), 0 ) if qj = 0
QM[j] Ü ( shl( QM[j-1] ), r-1 )
Q[j] Ü ( shl( QM[j-1] ), r - |qj| ) if qj < 0
QM[j] Ü ( shl( QM[j-1] ), (r-1) - |qj| )
where, for example, Q[j] Ü ( shl( Q[j-1] ), qj ) means that the register Q at iteration j is shifted one digit to the left and the last digit is loaded with qj. In QM, the current digit is given by qj - 1 mod r. Table 2.1 shows an example of conversion for radix-4 and a = 2.
|
| j | qj | Q | QM | ||||
| 1 | 1 | xxxxxxxx1 | xxxxxxxx0 | |||||
| 2 | 2 | xxxxxxx12 | xxxxxxx11 | |||||
| 3 | 0 | xxxxxx120 | xxxxxx113 | |||||
| 4 | -1 | xxxxx1133 | xxxxx1132 | |||||
| 5 | 0 | xxxx11330 | xxxx11323 | |||||
| 6 | 0 | xxx113300 | xxx113233 | |||||
| 7 | 2 | xx1133002 | xx1133001 | |||||
| 8 | -2 | x11330012 | x11330011 | |||||
| 9 | -1 | 113300113 | 113300112 | |||||
Register QP is updated every iteration by the following rules:
QP[j] Ü ( shl( QP[j-1] ), 0 ) qj = r-1
QP[j] Ü ( shl( Q[j-1] ), qj+1 ) -1 £ qj £ r-2
QP[j] Ü ( shl( QM[j-1] ), r-|qj|+1 ) qj < -1
In the last iteration the rounding of the bit in the least-significant position is performed as follows. First the quotient digit qm is converted into
|
Finally, the quotient is obtained by
| (10) | |||||||||||||||
|
| qm | SIGN | ZERO | p | case |
| r-1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | |
| 1 | - | r-1 | 2 | |
| 0 £ qm < r-1 | 0 | 0 | gm + 1 | 2 |
| 0 | 1 | gm + G1 | 2 | |
| 1 | - | gm | 2 | |
| -1 | 0 | - | 0 | 2 |
| 1 | - | r-1 | 3 | |
| qm < -1 | 0 | 0 | gm + 1 | 3 |
| 0 | 1 | gm + G1 | 3 | |
| 1 | - | gm | 3 | |
We now show an example of application of the division algorithm for the case of radix-4 with a = 2. The selection function is given in Table 2.3. The quotient digit h selected is the one satisfying the expression mh £ [^y] < mh+1. The example, shown in Table 2.4, is for the division x/d with x = 0.5 and d = 0.6 = 0.10011001... (binary) which produces q = 0.8[`3]. The binary value of dd (d = 3) is 001. The bit of weight 2-1 is always omitted because it is always 1 for the normalization 1/2 £ d < 1. Values in table, except qj+1, are given as hexadecimal vectors.
| mh | dd | |||||||
| 8/16 | 9/16 | 10/16 | 11/16 | 12/16 | 13/16 | 14/16 | 15/16 | |
|
m2 | 0C | 0E | 0F | 10 | 12 | 14 | 14 | 18 |
| m1 | 04 | 04 | 04 | 04 | 06 | 06 | 08 | 08 |
| m0 | 7C | 7A | 7A | 7A | 78 | 78 | 78 | 78 |
| m-1 | 73 | 71 | 70 | 6E | 6C | 6C | 6A | 68 |
| Values in table (multiplied by 16) are in hexadecimal | ||||||||
|
|
j y q_j -q_j d Ws Wc q
------------------------------------------------------------------------------
0 00 0 000000000000000 020000000000000 000000000000000 00000000000000
1 08 1 366666600000000 1E66665FFFFFFFF 000000000000001 00000000000001
2 79 -1 099999A00000000 100000DFFFFFFF8 133332400000008 00000000000003
3 0C 1 366666600000000 1AAAAC20000003F 088886BFFFFFFC1 0000000000000D
4 0C 1 366666600000000 1EEECC200000007 044465BFFFFFFF9 00000000000035
5 0C 1 366666600000000 1CCCC0200000007 06666DBFFFFFFF9 000000000000D5
6 0C 1 366666600000000 1CCCD0200000007 06664DBFFFFFFF9 00000000000355
7 0C 1 366666600000000 1CCC10200000007 0666CDBFFFFFFF9 00000000000D55
8 0C 1 366666600000000 1CCD10200000007 0664CDBFFFFFFF9 00000000003555
9 0C 1 366666600000000 1CC110200000007 066CCDBFFFFFFF9 0000000000D555
10 0C 1 366666600000000 1CD110200000007 064CCDBFFFFFFF9 00000000035555
11 0C 1 366666600000000 1C1110200000007 06CCCDBFFFFFFF9 000000000D5555
12 0C 1 366666600000000 1D1110200000007 04CCCDBFFFFFFF9 00000000355555
13 0C 1 366666600000000 111110200000007 0CCCCDBFFFFFFF9 00000000D55555
14 77 -1 099999A00000000 1EEEEFDFFFFFFF8 022221400000008 00000003555553
15 03 0 000000000000000 13333A7FFFFFFC0 11110A000000040 0000000D55554C
16 10 2 2CCCCCC00000000 04440D4000001FF 1999D17FFFFFE01 00000035555532
17 77 -1 099999A00000000 1EEEE95FFFFFFF8 02222B400000008 000000D55554C7
18 03 0 000000000000000 1333087FFFFFFC0 11114A000000040 0000035555531C
19 10 2 2CCCCCC00000000 0445C54000001FF 1998517FFFFFE01 00000D55554C72
20 77 -1 099999A00000000 1EEFC95FFFFFFF8 02222B400000008 000035555531C7
21 03 0 000000000000000 1337887FFFFFFC0 11104A000000040 0000D55554C71C
22 10 2 2CCCCCC00000000 0453C54000001FF 1998517FFFFFE01 00035555531C72
23 77 -1 099999A00000000 1EB7C95FFFFFFF8 02922B400000008 000D55554C71C7
24 04 1 366666600000000 06F1EE20000003F 149C4ABFFFFFFC1 0035555531C71D
25 6D -2 133333400000000 1A85A13FFFFFFF8 06E675800000008 00D55554C71C72
26 05 1 366666600000000 07E934A0000003F 142D8CBFFFFFFC1 035555531C71C9
27 6F -2 133333400000000 1C21D33FFFFFFF8 076C65800000008 0D55554C71C722
28 0D 1 366666600000000 1B50BCA0000003F 094E8CBFFFFFFC1 35555531C71C89
29 rounding step: sign (ws + wc) = 0 --> add 1 1
35555531C71C8A
Table 2.4: Example of radix-4 division.
As the radix increases the number of iterations needed to compute the quotient of the division are reduced, but the selection function becomes more complicated.
Higher radices can be obtained by executing several recurrence iterations in the same cycle. This produces more bits of the result per cycle. However, the cycle time is lengthened and its longer delay offsets the benefit of having a reduced number of cycles. The only reduction in time is due to register loading that is done once for cycle. As an alternative, lower radices stages can be overlapped to reduce the cycle time and the latency of division [10,,]. When the delay in the selection function is dominant over the delay of the other components of the recurrence (carry-save adders, multiple generators, multiplexers) it might be convenient to replicate and overlap more selection functions.
In the case shown in Figure 2.3, two stages are overlapped. The first stage produces qj+1 which is used to select qj+2 among all the possible combination of [^y]j+1 = trunc (rw[j]-qj+1d). Because only a few bits of the carry-save representation of w are needed in the selection function, all [^y]s can be obtained by small CSAs at the input of the selection functions (one for each possible value of qj+1). For example, for a = 2 five selection functions and four small CSAs are required to generate qj+2. The resulting quotient digit, for the scheme of Figure 2.3, is rqj+1 + qj+2.

Figure 2.3: Selection function with overlapped stages.
Because of the replication of the selection function, which number is proportional to a, the radices which are suitable to be overlapped are 2 and 4. The drawback of this scheme is the use of hardware duplication and, therefore, a resulting larger area.
Another division unit studied is the digit-recurrence algorithm radix-512 with scaling and quotient-digit selection by rounding, presented in [10,]. The unit, implemented in [33], showed a speed-up of about 2.0 over the radix-4 divider. Although radix-512 belongs to the category of the digit-recurrence algorithms, the implementation is quite different from the ones for lower radices and some structures such as recoders and trees of adders are present.
For radix-512 nine bits of the quotient are produced every iteration. To apply the quotient-digit selection by rounding, the divisor must be within a determined range. To achieve this, both operands are scaled by a quantity M » [1/d] so that:
|
|
|
|
|
|
|
|
|
|
The residual w[j] is in carry-save representation to avoid carry-propagation in the addition and the quotient-digit qj+1 is also in carry-save representation before the recoding. The multiplication qj+1z is performed by recoding one of the operands. This recoding is done from the carry-save representation of the shifted residual and the recoder also produces the quotient-digit obtained by the rounding of two fractional bits of the shifted residual [32]. The recoded operand is in signed digit representation and each digit can assume the values { -2, -1, 0, 1, 2 }.

Figure 2.4: Block diagram of radix-512 divider.
The algorithm, represented by the block diagram in Figure 2.4, is divided into four parts:
for a total of ten iterations needed to perform one division.
An example of application of the radix-512 division algorithm is shown in Table 2.5, The division of x = 0.5 and d = 0.6 produces q = x/d = 0.8[`3]. Values in table, except qj+1 and z, are given as hexadecimal vectors.
|
|
j q_j ys Ws yc Wc q
---------------------------------------------------------------------------
- Ms = 7557 Mc = 5550
- - 379B|262DD97FFFFFC0 1065|66A44900000040 00000000000000 z = 1.0002595 dec
0 - 3540|DFFFFFFFFFFFC0 116A|40000000000040 00000000000000
1 427 3A2A|E07F0B7FFFF000 032A|3D016900001000 000000000001AB
2 -341 2D66|FEF9F4807FFFF0 1532|124C16FF800010 00000000035555
3 166 3E30|F52F5EFFFFFFC0 0396|46A54200000040 00000006AAAAA6
4 114 3986|89595CFFFFFFE0 04B2|6A554600000020 00000D55554C72
5 -398 3DD5|C83612FFFFFF80 0450|4AA34A00000080 001AAAAA98E38E
6 136 3D05|A1B2768003FFF0 06D4|B49312FFFC0010 35555531C71C89
rounding step: sign (ws + wc) = 0 --> add 1 1
35555531C71C8A
Table 2.5: Example of radix-512 division.
The algorithm to compute the square root is quite similar to the division one. It is implemented, as described in [10], by the recurrence
| (11) |
|
|
By comparing expression (2.5) with expression (2.1), the term inside ( ) in expression (2.5) substitutes qj+1d in expression (2.1). Because of these similarities in the recurrence, it is convenient to implement division and square root in the same unit as discussed next.
Because of the similarities in the algorithm, division and square root can be effectively implemented in the same unit [31,,]. The combined division and square root, described in detail in [10], is implemented by the residual recurrence
| (12) |
| (13) | ||||||||||||||
| ||||||||||||||
| ||||||||||||||||
|
The recurrence is implemented, as shown in Figure 2.5 with the selection function (SEL), the block to form F (FGEN), a block (DSMUX) which provides FGEN with the appropriate bit vectors3 (depending on the operation selected by signal OP), a carry-save adder (CSA), and two registers to store the carry-save representation of the residual. The conversion block performs the conversion from signed-digit to conventional representation and the rounding. The result is rounded in the last iteration according to the sign of the final residual and the signal that detects if it is zero, which are produced by the sign-zero-detection block (SZD).
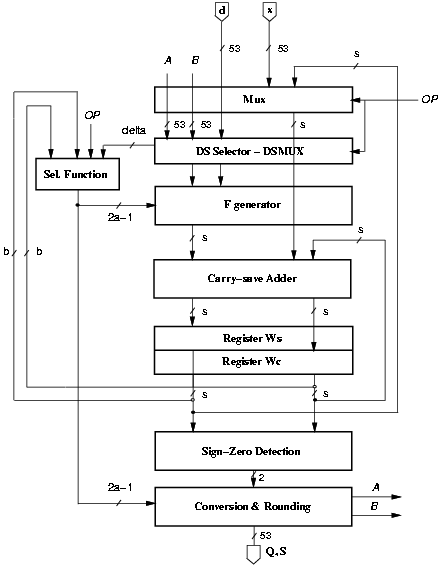
Figure 2.5: Combined division/square root unit.
2 Because in IEEE standard floating-point quantities are normalized in [1,2) it is necessary to right-shift the operands one position. Furthermore, if x ³ d, x is right-shifted an extra position (pre-shifting).
3 In special cases, such as for radix-2 and 4, one bit vector is sufficient.