|
R
N
S
Residue Number System
resources
| |
preliminary /
under construction |
Background
A Residue Number System (RNS) is defined by a set of P relatively
prime integers { m1, m2, ... , mP } which identify the
RNS base. Its
dynamic range is given by the product
Any integer X ∈
{ 0, 1, 2, ... , M-1 } has a unique RNS representation given by:
where < X >mi denotes the operation
X mod mi
[1].
Figure 1
illustrates an example of RNS, with base
{ 5, 7, 8 } and dynamic range M=5 · 7 · 8 = 280,
and how a positive integer is mapped into the RNS.
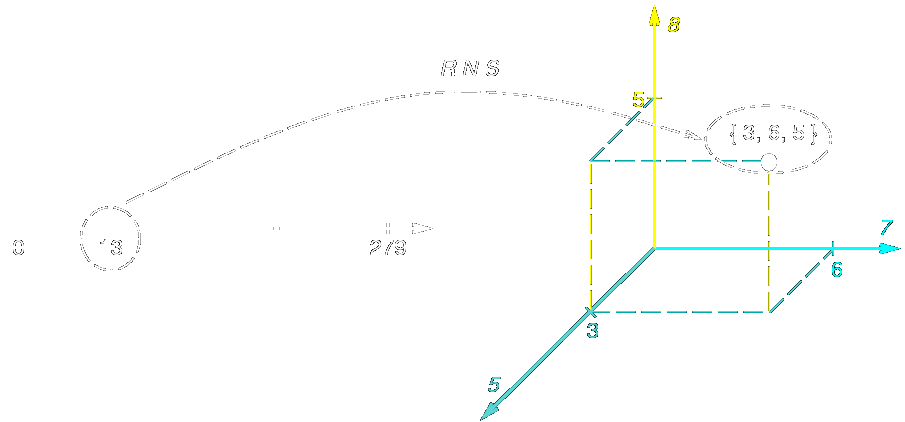 Figure 1: Architecture of the modular adder.
Figure 1: Architecture of the modular adder.
The conversion from the RNS representation to the integer one can be accomplished by
the Chinese Remainder Theorem (CRT):
| with | 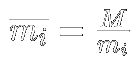 | and |  | . |
Operations, such as addition and multiplication, are computed independently
(parallel) in each path modulus mi
As a consequence, operations on large wordlengths (2k ≤ M)
can be split
into several modular operations executed in parallel and with
reduced wordlength (2k ≤
mi) [1].
Therefore, a digital system can be implemented in RNS
by decomposing it into P data-paths working in parallel,
as sketched in Figure 2.
 Figure 2: Architecture of RNS FIR filters.
Figure 2: Architecture of RNS FIR filters.
Resources
 Example
of RNS addition using the base of Figure 1.
Example
of RNS addition using the base of Figure 1.
 RNS Addition Applet
RNS Addition Applet
[Home]
< Previous
Next >
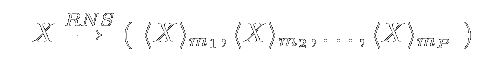


 Example
of RNS addition using the base of Figure 1.
Example
of RNS addition using the base of Figure 1.
 RNS Addition Applet
RNS Addition Applet