| R N S Residue Number System resources |
preliminary / under construction |
|---|
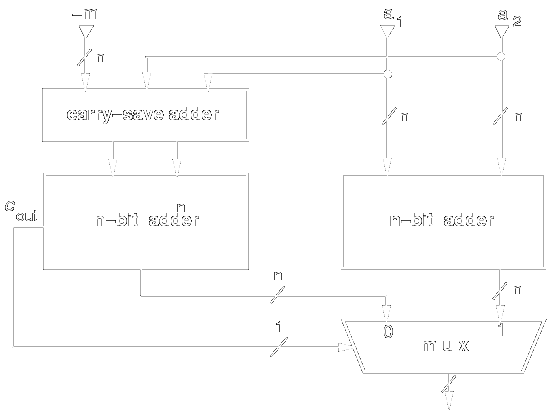
The above algorithm can be implemented by the most general architecture
shown in Figure 3.
Clearly, the modular adder is simplified when:
The scheme of Figure 3
is very general and several methods have been presented to efficiently implement the correction -m
[3]Modular Addition
The easiest way to implement two-operand modular addition, for any modulus m,
is to perform two additions modulus 2k (with m ≤ 2k).
If the result of a1 + a2 exceeds the modulus, by subtracting m we obtain
the correct result.
To speed-up the operation we can execute in parallel the two operations:
< a1 + a2 >m
If the sign of the three-term addition is negative, it means than the sum
(a1 + a2) < m and the modular sum is a1 + a2,
otherwise the modular addition is the result of the three-term addition.
(a1 + a2) and (a1 + a2 - m).

 Addition Applet
Addition Applet