| R N S Residue Number System resources |
preliminary / under construction |
|---|
One of the advantages of the use of moduli of small dynamic range which
are prime numbers, is that we can transform modular multiplication into
a modular addition by the isomorphism technique [2].
The isomorphic transformation is based on the concept of indices that are
similar to logarithms, and primitive roots r which are similar to logarithm bases.
It is possible to demonstrate that if the number m is prime there exists a number of primitive radices (the number of the primitive radices can be computed by using the Euler's function) that share the following property: every element of the field
F(m) = {0, 1, ..., m-1
excluding the zero element can be generated by using the following equation
Modular Multiplication
where k is an integer number.
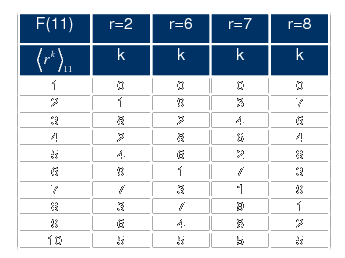
In Figure 4 the generation of the elements for
F(11) is shown. In this case the four primitive radices
{2, 6, 7, 8} can be utilized.
F(m) =
< rk
>m (7)

The product of two elements a1 and a2 belonging to the field is implemented by
If the modulus is small (its representation is six or seven bits), the forward and reverse transformations can be implemented by look-up table of reasonable size which are then synthesized into multi-level combinational logic.
Therefore, the product of
a1 and a2 modulo m can be obtained as:
|
|
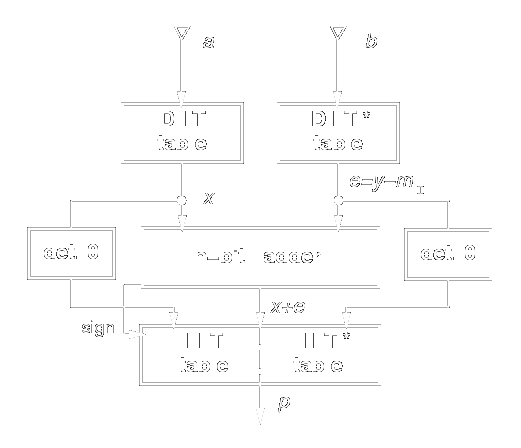
The architecture of the isomorphic multiplier is shown in Figure 5.

An alternative for isomorphic multiplication was proposed in [5]. Because isomorphic multipliers use modular adders in combination with tables, one of the adders in Figure 3 is eliminated and the modulus operation is incorporated in the IIT table. Moreover, the addition of the constant -mI is incorporated in one of DIT tables (called DIT*), as well. The resulting scheme, shown in Figure 6, is faster and consumes less power, as detailed in [5].
 Multiplication by Isomorphism Applet
Multiplication by Isomorphism Applet