Jeppe Revall Frisvad Associate Professor in Computer Graphics, M.Sc.(Eng.), Ph.D. Visual Computing DTU Compute Technical University of Denmark Contact information Home Publications Teaching Code Packages Press Appearances

Code Packages

dirpole (C++)	Code for computing subsurface scattering using direct Monte Carlo integration. This code is a simplistic implementation of our directional dipole model for subsurface scattering. A more complete implementation can be obtained by incorporating the model into the 02941 render framework (see below).
(WebGL)	We also provide a WebGL visualization of the diffuse reflectance returned by the directional dipole model as a function of various input parameters. The webpage enables interactive modification of optical properties and angle of incidence. Press F12 with the webpage in focus and find the file dirsss.js to have a look at the implementation in the browser (it includes evaluation of the directional dipole BSSRDF in a GLSL shader).
	Related references:
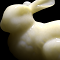
	Dal Corso, A., Frisvad, J. R., Mosegaard, J., Bærentzen, J. A. Interactive directional subsurface scattering and transport of emergent light. The Visual Computer 33(3), pp. 371-383, March 2017. [abstract] [video] [lowres pdf]
	Frisvad, J. R., Hachisuka, T., and Kjeldsen, T. K. Directional dipole model for subsurface scattering. ACM Transactions on Graphics 34(1), pp. 5:1-5:12, November 2014. Presented at SIGGRAPH 2015. [abstract/demo] [code] [lowres pdf]
	Frisvad, J. R., Hachisuka, T., and Kjeldsen, T. K. Directional Dipole for Subsurface Scattering in Translucent Materials. Manuscript, August 2013. [lowres pdf]
02941 Render	Rendering framework for the course 02941 Physically Based Rendering and Material Appearance Modelling. The framework is incomplete in its publicly available form. Work through the exercises at the course webpage to complete it. The package includes a Visual Studio 2013 solution and CMake files for compiling on various platforms. LMabs (see below) is incorporated into the optprops part of this framework.
onb (C++)	Code for building an orthonormal basis from a 3d unit vector without explicit normalization. This code is at least 50% faster than methods which are based on vector normalization and cross product. The method is very useful for rotating a direction sampled around the z-axis (using spherical coordinates, for example) to a direction sampled around an arbitrary vector. I used it for importance sampling the Rayleigh phase function and it is also included in the file sampler.h of the 02941 render framework (see above). The new function for computing an orthonormal basis is also included in the math library (CGLA) of the GEL framework (see below).
(WebGL)	It turns out that this technique for building an orthonormal basis is also very useful for generating a consistently oriented tangent space. To demonstrate this, I used it to comb a hairy ball in a small WebGL demo. Press F12 with the webpage in focus and find the file hairy.js to have a look at the implementation in the browser.
	Related references:
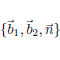	Frisvad, J. R. Building an orthonormal basis from a 3d unit vector without normalization. Journal of Graphics Tools 16(3), pp. 151-159, August 2012. [onb code] [abstract] [demo]
	Frisvad, J. R. Importance sampling the Rayleigh phase function. Journal of the Optical Society of America A 28(12), pp. 2436-2441, December 2011.
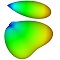
LMabs (C++)	Code for computing the scattering properties of participating media using Lorenz-Mie theory. This code handles both absorbing particles and an absorbing host. Code that computes the scattering properties of milk as a function of fat and particle content is included as an example. The scattering properties of milk are computed both per wavelength and in RGB. Most of the images in the related references (listed just below) used the RGB properties. A full spectral rendering of a milk splash has been generated using optical properties from this code.
(Matlab)	A Matlab version is now available. It is very slow compared to the original C++ version, but it is convenient to have the code in Matlab for plotting purposes. The original code finds the asymmetry parameter g in place of the phase function. The Matlab version also includes functions for evaluating and plotting the actual Lorenz-Mie phase function.
(WebGL)	I also provide 3D visualization of the Lorenz-Mie phase function. This WebGL demo includes a partial implementation of the LMabs code in JavaScript (to get Lorenz-Mie coefficients), and the phase function is evaluated in WebGL shaders.
inhLMabs (Matlab)	The visualizer includes a new technique described in the reference given below [Frisvad 2018]. This is a technique for calculating the phase function of a spherical particle when scattering an inhomogeneous electromagnetic plane wave (it also works for homogeneous waves and thus includes the standard Lorenz-Mie phase function as a special case). There is also a Matlab implementation of this technique (called inhLMabs).
	Related references:
	Frisvad, J. R., Christensen, N. J., and Jensen, H. W. Computing the scattering properties of participating media using Lorenz-Mie theory. ACM Transactions on Graphics (Proceedings of ACM SIGGRAPH 2007) 26(3), pp. 60:1-60:10, July 2007.
	Frisvad, J. R. Light, Matter, and Geometry: The Cornerstones of Appearance Modelling, PhD thesis, Department of Informatics and Mathematical Modelling, Technical University of Denmark, May 2008.
	Frisvad, J. R., Christensen, N. J., and Jensen, H. W. Predicting the appearance of materials using Lorenz–Mie theory. In W. Hergert and T. Wriedt, eds., The Mie Theory: Basics and Applications, Springer Series in Optical Sciences, Vol. 169, Chapter 4, pp. 101-133, July 2012. [abstract]
	Dal Corso, A., Frisvad, J. R., Kjeldsen, T. K., and Bærentzen, J. A. Interactive appearance prediction for cloudy beverages. In Workshop on Material Appearance Modeling (MAM2016), pp. 1-4, The Eurographics Association, June 2016.
	Frisvad, J. R. Phase function of a spherical particle when scattering an inhomogeneous electromagnetic plane wave. Journal of the Optical Society of America A 35(4), pp. 669-680. April 2018.
noise (WebGL)	Different implementations of the noise function as a GLSL ES function without lookup tables. This WebGL demonstrator enables exploration of the noise functions using the mouse, so that one can visually inspect noise quality. The sparse convolution noise function of Frisvad and Wyvill [2007] (as implemented in this demo) is described as a functional expression by Luongo et al. [2020] and used for modification of surface microstructure in a 3D printing process.
	Related references:
	Luongo, A., Falster, V., Doest, M. B., Ribo, M. M., Eiriksson, E. R., Pedersen, D. B., and Frisvad, J. R. Microstructure control in 3D printing with digital light processing. Computer Graphics Forum 39(1), pp. 347-359. February 2020. [lowres pdf]
	Frisvad, J. R., and Wyvill, G. Fast high-quality noise. In Proceedings of GRAPHITE 2007, ACM, pp. 243-248+315, December 2007. [video MPEG/QT] [WebGL demo]
	Wyvill, G., and Frisvad, J. R. Better faster noise with the GPU. In ACM SIGGRAPH 2007 Posters, Article 180, July 2007. [abstract] [video MPEG/QT]
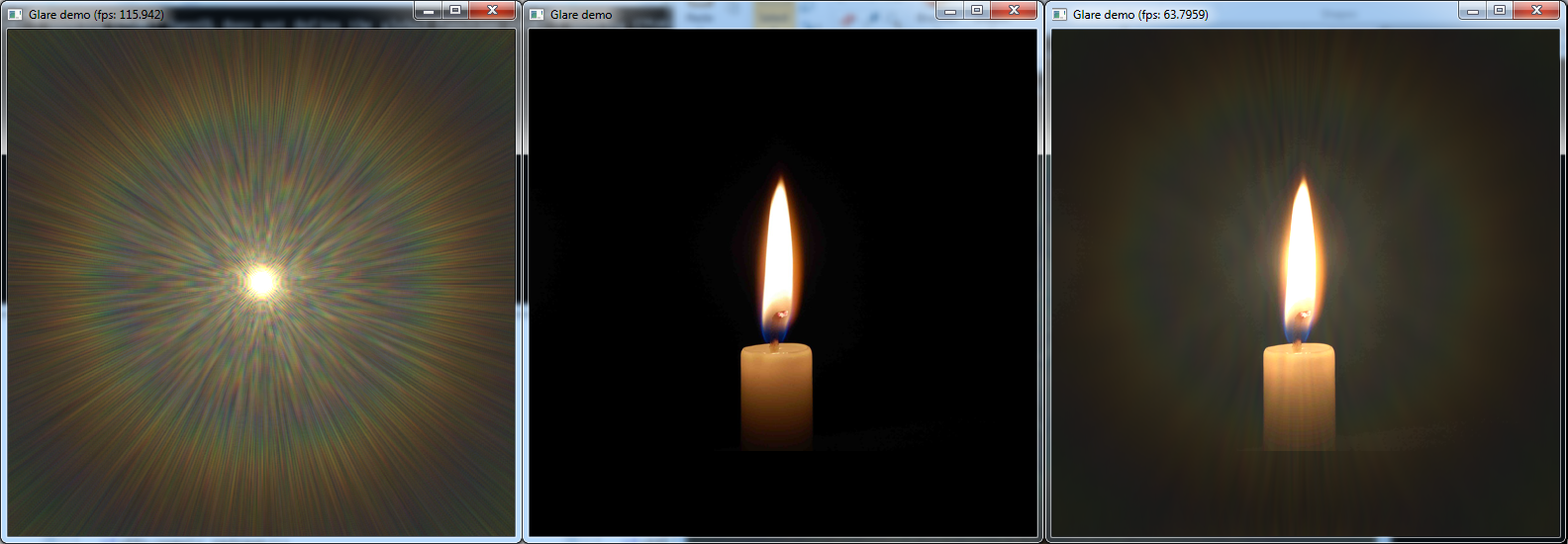
Glare demo	Real-time GPU implementation of the glare resulting from the scattering in the human eye. This demo includes a human aperture model, Fresnel diffraction, chromatic blur, convolution, and pupillary hippus. It is thus a partial implementation of the glare method described in the paper referenced below. The program takes an image and a bright pixel overlay as input and adds the convolution of the diffraction pattern (the point spread function) and the bright pixel overlay to the input image.
Pupillary hippus	WebGL demonstrator of my procedural model for simulating pupillary hippus. The implementation uses sparse convolution noise as the noise function (see demonstrator above). The webpage includes a (slow) Matlab implementation.
	Related references:
	Ritschel, T., Ihrke, M., Frisvad, J. R., Coppens, J., Myszkowski, K., and Seidel, H.-P. Temporal glare: Real-time dynamic simulation of the scattering in the human eye. Computer Graphics Forum (Proceedings of Eurographics 2009) 28(2), pp. 183-192, April 2009.
	Trester, S. Computer-simulated Fresnel diffraction using the Fourier transform. Computing in Science & Engineering 1(5), pp. 77-83, September/October 1999.
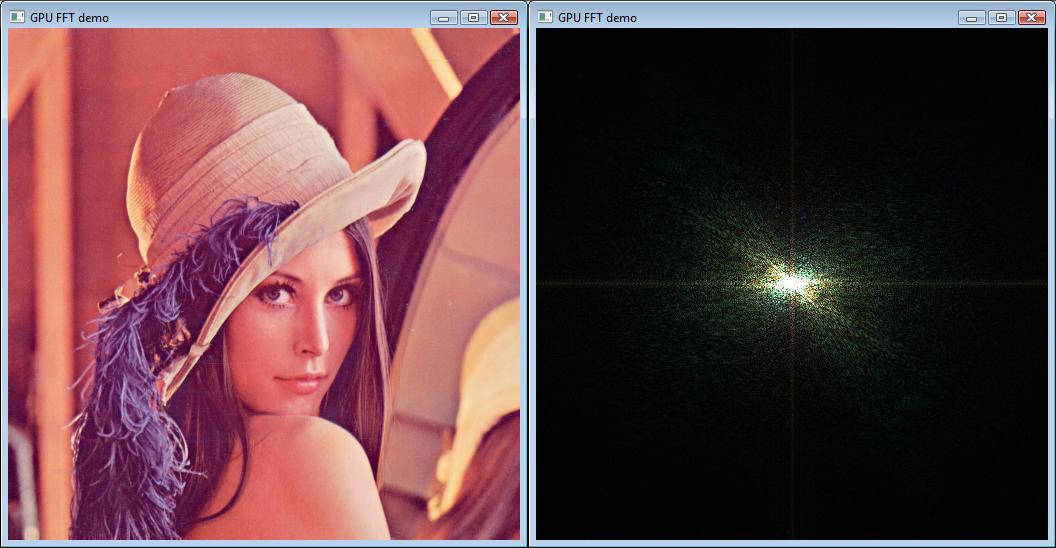
GPU FFT	The GPU is extremely efficient at computing the Discrete Fourier Transform. Because of its roots in graphics, it is particularly well-suited for working with 4-vectors. This means that two DFTs in parallel is a very good idea (two complex numbers in each 4-vector). If we implement two parallel FFTs in GLSL using the classic Cooley-Tukey algorithm, we compute the 2D FFT of an 512x512 RGB image in 2 milliseconds using only a laptop GPU (NVIDIA Quadro FX 1600M).
	Related references:
	Sørensen, H. H. B., Glimberg, S., Hansen, T. J., Frisvad, J. R., Engsig-Karup, A. P. Development of desktop computing applications and engineering tools on GPUs. GPU Technology Conference 2010 Posters, September 2010.
	Sumanaweera, T., Liu, D. Medical Image Reconstruction with the FFT. In GPU Gems 2: Programming Techniques for High-Performance Graphics and General-Purpose Computation, Chapter 48, pp. 765-784, 2005.
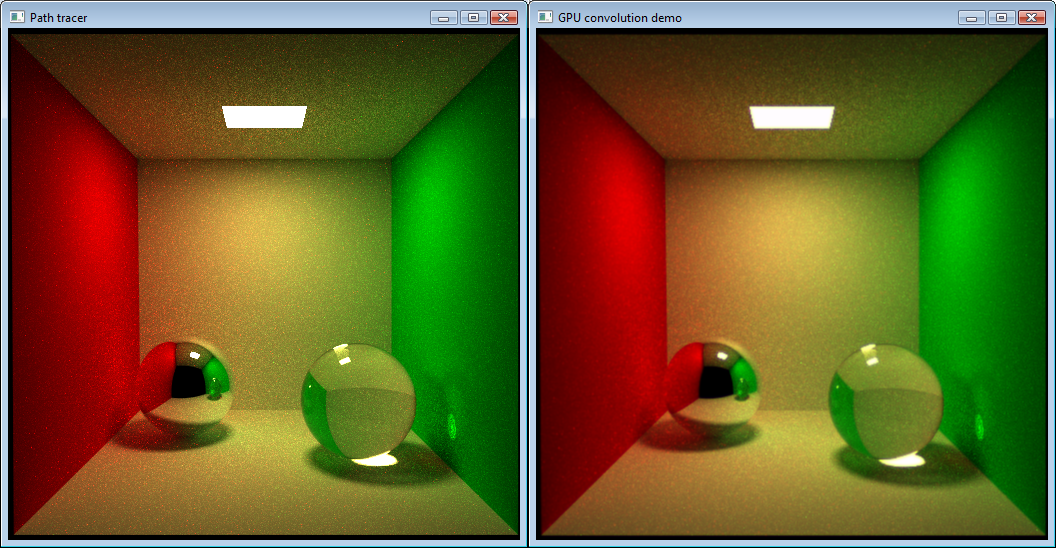
GPU convolution	Using the GPU FFT implementation, we can easily implement convolution on the GPU. Here the two parallel FFTs become a great advantage since we can compute the FFT of corresponding colour bands in parallel and multiply them immediately after. We need nine 2D FFTs to convolve two RGB images. The images below illustrate how we can use convolution to reduce the high-frequency noise which often appears in images rendered using classic Monte Carlo path tracing. The filter image is computed procedurally on the GPU in this example. Convolution of two 512x512 RGB images takes only 5.5 milliseconds using a laptop GPU (NVIDIA Quadro FX 1600M).
	Related references:
	Sørensen, H. H. B., Glimberg, S., Hansen, T. J., Frisvad, J. R., Engsig-Karup, A. P. Development of desktop computing applications and engineering tools on GPUs. GPU Technology Conference 2010 Posters, September 2010.
GEL	GEL (Graphics Elements Library, in my opinion) is a framework for computer graphics and 3D vision. It is mostly the work of Andreas Bærentzen, but I have also contributed some minor parts. Some parts of GEL are used in the 02941 Render framework.

Old Projects

Boxer!	Student project about making artificial intelligence (AI) for a simplistic boxing game. The implemented AI actually works quite well. It is based on cognitive modelling and the STRIPS algorithm for planning the next actions. A heuristic method is included to incorporate learning, such that the AI controlled boxers improve over time. Webpage is in Danish. Code is implemented in Pascal (Delphi).